题目内容

3．在实数$\frac{22}{7}$，$\root{3}{4}$，$\sqrt{9}$，π，2$\sqrt{2}$中，无理数有3个．

分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．

解答 解：无理数有：$\root{3}{4}$，π，2$\sqrt{2}$共3个．
故答案是：3．

点评 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．

练习册系列答案
相关题目
13．（1）如图1，已知⊙O的半径是4，△ABC内接于⊙O，AC=4$\sqrt{2}$．
①求∠ABC的度数；
②已知AP是⊙O的切线，且AP=4，连接PC．判断直线PC与⊙O的位置关系，并说明理由；
（2）如图2，已知?ABCD的顶点A、B、D在⊙O上，顶点C在⊙O内，延长BC交⊙O于点E，连接DE．求证：DE=DC．
14．在函数y=$\frac{2}{x}$，y=x+5，y=-5x的图象中，是中心对称图形，且对称中心是原点的图象的个数有（　　）
A．0个B．1个C．2个D．3个
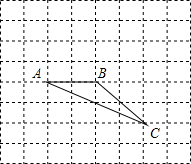11．如图在8×8的正方形网格中，△ABC 的顶点在边长为1的小正方形的顶点上．
（1）?填空：∠ABC=135°，BC=2$\sqrt{2}$．
（2）若点A在网格所在的坐标平面里的坐标为（1，-2），请你在图中找出一点D，并作出以A、B、C、D四个点为顶点的平行四边形，求出满足条件的D点的坐标．
18．若a是（-8）2的平方根，则$\root{3}{a}$等于（　　）
A．-8B．2C．2或-2D．8或-8
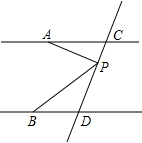8．如图，已知AC∥BD，点P是直线CD上的一个动点（P点与点C、D不重合）
（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD之间有什么关系，这种关系是否发生变化？
（2）若点P在C、D两点的外侧运动时，试探索∠PAC，∠APB，∠PBD之间的关系又是如何？
15．将下列各式分解因式：
（1）4x2-y2
（2）x3-10x2+25x．
12．（1）计算：（$\sqrt{48}$-4$\sqrt{\frac{1}{8}}$）-（3$\sqrt{\frac{1}{3}}$-2$\sqrt{0.5}$）
（2）化简：（$\sqrt{{a}^{3}b}$-$\sqrt{\frac{a}{b}}$+2$\sqrt{\frac{b}{a}}$+$\sqrt{ab}$）÷$\sqrt{\frac{b}{a}}$．
13．已知方程组$\left\{\begin{array}{l}{ax+by=10}\\{mx-ny=8}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，求方程组$\left\{\begin{array}{l}{\frac{a}{2}（x+y）+\frac{b}{3}（x-y）=10}\\{\frac{m}{2}（x+y）+\frac{n}{3}（x-y）=8}\end{array}\right.$的解．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网