题目内容
18.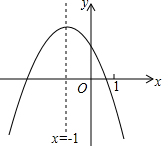 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1),
其中错误的结论是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
分析 ①根据图象与x轴有2个交点,可知b2-4ac>0,判断①;
②根据x=1时,y<0和对称轴是x=-1,判断②;
③根据x=-2时,y>0,判断③;
④根据当x=-1时,y有最大值a-b+c,列式判断④.
解答 解:①图象与x轴有2个交点,依据根的判别式可知b2-4ac>0,则4ac-b2<0,①正确;
②-$\frac{b}{2a}$=-1,∴a=$\frac{1}{2}$b,
x=1时,y<0,∴a+b+c<0,
即$\frac{1}{2}$b+b+c<0,∴3b+2c<0,②正确;
③根据对称轴为x=-1,当x=-2时,y>0,∴4a-2b+c>0,即4a+c>2b,③不正确;
④当x=-1时,y有最大值a-b+c,
∴am2+bm+c<a-b+c,∴m(am+b)+b<a(m≠-1),④正确.
故选:C.
点评 本题考查的是图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用↑的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
6. 如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=( )
如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=( )
 如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=( )
如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=( )| A. | 25° | B. | 30° | C. | 35° | D. | 45° |
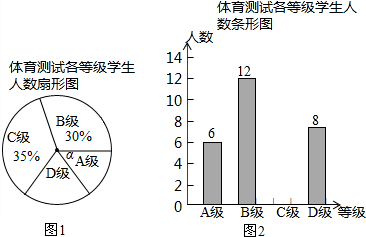
10.如图,某校合作学习小组随机抽样统计部分高年级男同学对必修球类“篮球、足球、排球”三大球的喜爱程度的人数,绘制出不完整的统计图表如下:
(1)试把表格中的数据填写完整:
(2)试利用上述表格中的数据,补充完成条形统计图的制作(用阴影部分表示);
(3)若再随机抽查该校高年级男学生一人,则该学生喜爱的三大球最大可能是什么.

(1)试把表格中的数据填写完整:
| 品牌 | 篮球 | 足球 | 排球 | 抽样人数合计 |
| 喜爱人数 | 36 | 24 | 20 | 80 |
| 百分比 | 45% | 30% | 25% | 100% |
(3)若再随机抽查该校高年级男学生一人,则该学生喜爱的三大球最大可能是什么.


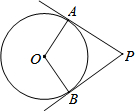 如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,PA=$6\sqrt{3}$,那么$\widehat{AB}$的长为4π.
如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,PA=$6\sqrt{3}$,那么$\widehat{AB}$的长为4π. 如图,⊙O是边长为4的等边△ABC的内切圆,D、E为切点,则图中阴影部分的面积为$\frac{4}{9}$π.
如图,⊙O是边长为4的等边△ABC的内切圆,D、E为切点,则图中阴影部分的面积为$\frac{4}{9}$π.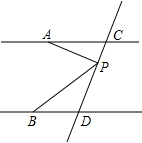 如图,已知AC∥BD,点P是直线CD上的一个动点(P点与点C、D不重合)
如图,已知AC∥BD,点P是直线CD上的一个动点(P点与点C、D不重合)