题目内容
6. 如图,已知?ABCD和?ABEF,连接AC、DF、CE、AE,AC与DF交于点G,若AC=DF=AE.
如图,已知?ABCD和?ABEF,连接AC、DF、CE、AE,AC与DF交于点G,若AC=DF=AE.(1)求证:△AEC为等边三角形;
(2)求∠AGF的度数;
(3)若点F、B、C在同一直线上,求证:四边形ABEF为菱形.
分析 (1)直接利用平行四边形的性质和判定方法得出四边形FDCE是平行四边形,进而得出DF=EC,再利用已知求出答案;
(2)利用等边三角形的性质结合平行四边形的性质得出答案;
(3)利用等边三角形的性质结合平行四边形的对角线互相平分,进而得出AE⊥BF,即可得出答案.
解答 (1)证明:∵在?ABCD和?ABEF中,
∴AB$\stackrel{∥}{=}$EF,AB$\stackrel{∥}{=}$DC,
∴EF$\stackrel{∥}{=}$DC,
∴四边形FDCE是平行四边形,
∴FD=EC,
∵AC=DF=AE,
∴AE=AC=EC,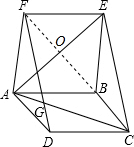
∴△AEC为等边三角形;
(2)解:∵△AEC为等边三角形,
∴∠ECA=60°,
∵四边形FDCE是平行四边形,
∴DF∥EC,
∴∠FGA=∠ECA=60°;
(3)证明:如图所示:连接FB,AE与BF相交于点O,
∵四边形ABEF是平行四边形,
∴AO=EO,
又∵△AEC为等边三角形,点F、B、C在同一直线上,
∴CO⊥AE,
∴AE⊥BF,
∴平行四边形ABEF是菱形.
点评 此题主要考查了平行四边形的判定与性质以及等边三角形的判定与性质,正确应用平行四边形的性质是解题关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
16.等腰三角形的两边长分别为4和7,则它的周长为( )
| A. | 18 | B. | 15 | C. | 15或18 | D. | 19 |
18.不等式1-2x<1 的解集是( )
| A. | x>-1 | B. | x<-1 | C. | x>1 | D. | x>0 |
15. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )| A. | 4$\sqrt{3}$ | B. | 5 | C. | 6 | D. | 6$\sqrt{3}$ |
 如图,∠BAF=40°,∠ACE=130°,CE⊥CD.问CD∥AB吗?为什么?
如图,∠BAF=40°,∠ACE=130°,CE⊥CD.问CD∥AB吗?为什么? 如图,在边长为1个单位长度的小正方形组成的网格中.
如图,在边长为1个单位长度的小正方形组成的网格中.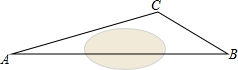 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)