题目内容
16.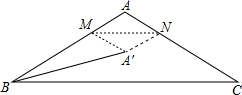 如图,在△ABC中,∠BAC=120°,AB=AC=4,点M,N分别在边AB,AC上,将△AMN沿MN翻折,点A的对应点为A′,连接BA′,则BA′长度的最小值为4$\sqrt{3}-4$.
如图,在△ABC中,∠BAC=120°,AB=AC=4,点M,N分别在边AB,AC上,将△AMN沿MN翻折,点A的对应点为A′,连接BA′,则BA′长度的最小值为4$\sqrt{3}-4$.
分析 首先求得BC的长度,然后由两点之间线段最短可知:当点B、N、C、A′在同一条直线上时,BA′的长度最小,然后根据BA′=BC-A′C求解即可.
解答 解:如图所示过点A作AD⊥BC于点D.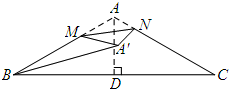
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=$\frac{1}{2}$×120°=60°,BD=DC.
∴sin∠BAD=$\frac{BD}{AB}=\frac{\sqrt{3}}{2}$,即$\frac{BD}{4}=\frac{\sqrt{3}}{2}$.
∴BD=2$\sqrt{3}$.
∴BC=4$\sqrt{3}$.
由翻折的性质可知:A′N=AN
∵AN+NC=AC=4,
∴A′N+NC=4.
要求BA′的最小值,只需BA′+A′N+NC有最小值,由两点之间线段最短可知:当点B、N、C、A′在同一条直线上时,BA′的长度最小.
如图所示: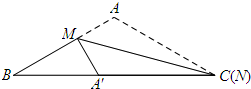
由翻折的性质可知:A′C=AC.
∴BA′=BC-A′C=4$\sqrt{3}$-4.
点评 本题主要考查的是翻折的性质、特殊度数的锐角三角函数值、线段的性质的应用,明确当点B、N、C、A′在同一条直线上时,BA′的长度最小是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.下列计算错误的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | C. | ${(\sqrt{3})^2}=3$ | D. | $(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})=1$ |
 已知,如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2.
已知,如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2. 张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿返回,途中在读报栏前看了一会儿报,此情景如图所示,请你回答下列问题:
张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿返回,途中在读报栏前看了一会儿报,此情景如图所示,请你回答下列问题: