题目内容
1．“三等分任意角”是数学史上一个著名问题，已知∠MAN，设∠α=$\frac{1}{3}$∠MAN．（1）若∠MAN=60°，则∠α的度数为20°．
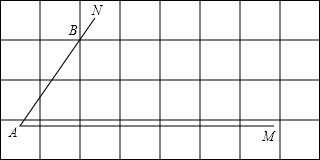
（2）如图，将∠MAN放置在每个小正方形的边长均为1cm的网格中，角的一边AM与水平方向的网格线平行，另一边AN经过格点B，且AB=2.5cm，现要求只能使用带刻度的直尺，请你在图中作出∠α，并简要说明作法．
分析 （1）根据题意，用60°乘以$\frac{1}{3}$，计算即可得解；
（2）根据直角三角形斜边上的中线等于斜边的一半可得斜边上的中线等于AB的长度，再结合三角形的外角性质可知，∠BAD=2∠BDC，再根据两直线平行，内错角相等可得∠BDC=∠MAD，从而得到∠MAD=$\frac{1}{3}$∠MAN．
解答 解：（1）∠α=$\frac{1}{3}$×60°=2O°，
故答案为：20°；
（2）如图所示：
让直尺有刻度一边过点A，设该边与过点B的竖直方向的网格线交于点C，与过点B水平方向的网格线交于点D，保持直尺有
刻度的一边过点A，调整点C、D的位置，使CD=5cm，画射线AD，此时∠MAD即为所求的∠α．
点评 本题考查了应用与设计作图，主要利用了直角三角形斜边上的中线等于斜边的一半的性质，使作出的直角三角形斜边上的中线恰好把三角形分成两个等腰三角形是解题的关键．
练习册系列答案
相关题目
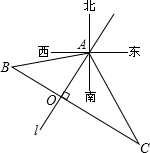一辆货车在公路BC上由B向C行驶，一辆小汽车在公路l上由A沿AO方向行驶．已知两条公路互相垂直，A到BC的距离为100米，两条公路的交点O位于A的南偏西32°方向上，点B位于A的南偏西77°方向上，点C位于A的南偏东28°方向上．设两车同时开出且小汽车的速度是货车速度的2倍，求两车在行驶过程中的最近距离．
生产车间现有一块如图所示的钢板料，现在要把它分成面积相等的两部分，请用一条直线画出切割线．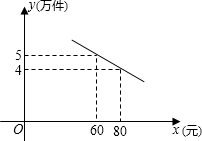
某通讯器材公司销售一种市场需求较大的新型通讯产品，已知每件产品的进价为40元，每年销售该种产品的总开支（不含进价）总计120万元，在销售过程中发现，年销售量y（万件）与销售单价x（元）之间存在着如图所示的一次函数关系．
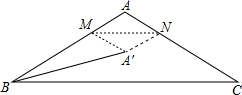如图，在△ABC中，∠BAC=120°，AB=AC=4，点M，N分别在边AB，AC上，将△AMN沿MN翻折，点A的对应点为A′，连接BA′，则BA′长度的最小值为4$\sqrt{3}-4$．
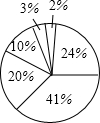根据如图的数据制作扇形统计图并回答问题
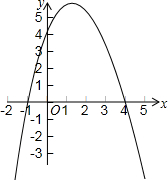已知二次函数y=-x2+3x+4的图象．