题目内容
6．$\frac{7}{25}$×（-$\frac{5}{6}$）$÷（-\frac{14}{5}）$．分析 根据有理数的乘法、除法，即可解答．
解答 解：$\frac{7}{25}×（-\frac{5}{6}）÷（-\frac{14}{5}）$
=$\frac{7}{25}×\frac{5}{6}×\frac{5}{14}$
=$\frac{1}{12}$．
点评 本题考查了有理数的乘法、除法，解决本题的关键是熟记有理数的乘法、除法的法则．
练习册系列答案
相关题目
16．
为了了解业余射击队队员的射击成绩，对某次射击比赛中每一名队员的平均成绩（单位：环，环数为整数）进行了统计．分别绘制了统计表和成绩分布直方图，请你根据统计表和成绩分布直方图回答下列问题：
（1）求出a，b，c的值；
（2）写出这次射击比赛成绩的众数与中位数．
为了了解业余射击队队员的射击成绩，对某次射击比赛中每一名队员的平均成绩（单位：环，环数为整数）进行了统计．分别绘制了统计表和成绩分布直方图，请你根据统计表和成绩分布直方图回答下列问题：| 平均成绩 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | a | 3 | 3 | b | 4 | c | 6 | 1 | 0 |
（2）写出这次射击比赛成绩的众数与中位数．
17．在0，1，$\frac{22}{7}$，-2，-3.5这五个数中，是非负整数的有（ ）个．
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
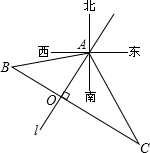一辆货车在公路BC上由B向C行驶，一辆小汽车在公路l上由A沿AO方向行驶．已知两条公路互相垂直，A到BC的距离为100米，两条公路的交点O位于A的南偏西32°方向上，点B位于A的南偏西77°方向上，点C位于A的南偏东28°方向上．设两车同时开出且小汽车的速度是货车速度的2倍，求两车在行驶过程中的最近距离．
15．
2014年全国两会民生活题再次成为社会焦点，央视记者为了了解百姓“两会民生话题”的聚焦点，随机调查了部分北京市民，并对结果进行整理．绘制了如下不完整的统计图表．
请根据图表中提供的信息解答下列问题：
（1）填空：这次调查的样本容量是400，m=40人；扇形统计图中，E组所对圆心角的度数为54°．
（2）北京市现常驻人口数达2000万，请估计关注D组话题的市民人数．
（3）若在这次接受调查的市民中，随机抽查一人，则此人关注C组话题的概率是多少？
2014年全国两会民生活题再次成为社会焦点，央视记者为了了解百姓“两会民生话题”的聚焦点，随机调查了部分北京市民，并对结果进行整理．绘制了如下不完整的统计图表． | 组别 | 焦点话题 | 人数 |
| A | 食品安全 | 80 |
| B | 教育医疗 | M |
| C | 就业养老 | 100 |
| D | 生态环保 | 120 |
| E | 其它 | 60 |
（1）填空：这次调查的样本容量是400，m=40人；扇形统计图中，E组所对圆心角的度数为54°．
（2）北京市现常驻人口数达2000万，请估计关注D组话题的市民人数．
（3）若在这次接受调查的市民中，随机抽查一人，则此人关注C组话题的概率是多少？
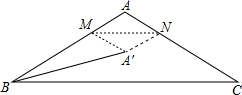如图，在△ABC中，∠BAC=120°，AB=AC=4，点M，N分别在边AB，AC上，将△AMN沿MN翻折，点A的对应点为A′，连接BA′，则BA′长度的最小值为4$\sqrt{3}-4$．