题目内容
4. 已知,如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2.
已知,如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2.(1)求∠2,∠3的度数.
(2)求长方形ABCD的纸片的面积S.
分析 (1)根据AD∥BC,∠1与∠2是内错角,因而就可以求得∠2,根据图形的折叠的定义,可以得到∠4=∠2,进而可以求得∠3的度数;
(2)已知AE=2,在Rt△ABE中,根据三角函数就可以求出AB、BE的长,BE=DE,则可以求出AD的长,就可以得到矩形的面积.
解答 解:(1)∵AD∥BC,
∴∠2=∠1=60°;
又∵∠4=∠2=60°,
∴∠3=180°-60°-60°=60°.
(2)在直角△ABE中,由(1)知∠3=60°,
∴∠5=90°-60°=30°;
∴BE=2AE=4,
∴AB=2$\sqrt{3}$;
∴AD=AE+DE=AE+BE=2+4=6,
∴长方形纸片ABCD的面积S为:AB•AD=2$\sqrt{3}$×6=12$\sqrt{3}$.
点评 此题考查了矩形的性质,折叠的性质以及直角三角形的性质.注意数形结合思想以及建模思想的运用是解题的关键.

练习册系列答案
相关题目
15. 2014年全国两会民生活题再次成为社会焦点,央视记者为了了解百姓“两会民生话题”的聚焦点,随机调查了部分北京市民,并对结果进行整理.绘制了如下不完整的统计图表.
2014年全国两会民生活题再次成为社会焦点,央视记者为了了解百姓“两会民生话题”的聚焦点,随机调查了部分北京市民,并对结果进行整理.绘制了如下不完整的统计图表.
请根据图表中提供的信息解答下列问题:
(1)填空:这次调查的样本容量是400,m=40人;扇形统计图中,E组所对圆心角的度数为54°.
(2)北京市现常驻人口数达2000万,请估计关注D组话题的市民人数.
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
 2014年全国两会民生活题再次成为社会焦点,央视记者为了了解百姓“两会民生话题”的聚焦点,随机调查了部分北京市民,并对结果进行整理.绘制了如下不完整的统计图表.
2014年全国两会民生活题再次成为社会焦点,央视记者为了了解百姓“两会民生话题”的聚焦点,随机调查了部分北京市民,并对结果进行整理.绘制了如下不完整的统计图表. | 组别 | 焦点话题 | 人数 |
| A | 食品安全 | 80 |
| B | 教育医疗 | M |
| C | 就业养老 | 100 |
| D | 生态环保 | 120 |
| E | 其它 | 60 |
(1)填空:这次调查的样本容量是400,m=40人;扇形统计图中,E组所对圆心角的度数为54°.
(2)北京市现常驻人口数达2000万,请估计关注D组话题的市民人数.
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
19.(-an)2n的结果是( )
| A. | -a3n | B. | a3n | C. | -${a}^{2{n}^{2}}$ | D. | ${a}^{2{n}^{2}}$ |
 生产车间现有一块如图所示的钢板料,现在要把它分成面积相等的两部分,请用一条直线画出切割线.
生产车间现有一块如图所示的钢板料,现在要把它分成面积相等的两部分,请用一条直线画出切割线.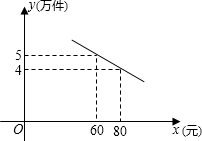 某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元,在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在着如图所示的一次函数关系.
某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元,在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在着如图所示的一次函数关系.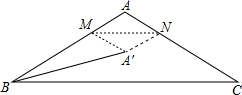 如图,在△ABC中,∠BAC=120°,AB=AC=4,点M,N分别在边AB,AC上,将△AMN沿MN翻折,点A的对应点为A′,连接BA′,则BA′长度的最小值为4$\sqrt{3}-4$.
如图,在△ABC中,∠BAC=120°,AB=AC=4,点M,N分别在边AB,AC上,将△AMN沿MN翻折,点A的对应点为A′,连接BA′,则BA′长度的最小值为4$\sqrt{3}-4$.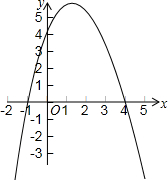 已知二次函数y=-x2+3x+4的图象.
已知二次函数y=-x2+3x+4的图象. 如图,AB∥CD,∠C=55°,CE⊥BE,垂足为E,则∠B的度数为35°.
如图,AB∥CD,∠C=55°,CE⊥BE,垂足为E,则∠B的度数为35°.