题目内容
7.观察下面各式:12+(1×2)2+22=(1×2+1)2
22+(2×2)2+32=(2×3+1)2
32+(3×4)2+42=(3×4+1)2
…
(1)写出第2005个式子;
(2)写出第n个式子,并说明你的结论.
分析 (1)仿照已知式子得出第2015个式子即可;
(2)以此类推得出第n个式子即可,进一步计算验证即可.
解答 解:(1)当n=1时,12+(1×2)2+22=(1×2+1)2;
当n=2时,22+(2×3)2+32=(2×3+1)2;
当n=3时,32+(3×4)2+42=(3×4+1)2;
…
第2005个式子即当n=2005时,有
20052+(2005×2006)2+20062=(2005×2006+1)2.
(2)第n个式子为n2+[n(n+1)]2+(n+1)2=[n(n+1)+1]2.证明如下:
∵n2+[n(n+1)]2+(n+1)2
=n2+n2(n+1)2+(n2+2n+1)
=n2+n2(n2+2n+1)+(n2+2n+1)
=n2+n4+2n3+n2+n2+2n+1
=n4+2n3+3n2+2n+1,
且[n(n+1)+1]2
=[n(n+1)2]+2[n(n+1)]•1+12
=n2(n+1)2+2n(n+1)+1
=n2(n2+2n+1)+2n2+2n+1
=n4+2n3+n2+2n2+2n+1
=n4+2n3+3n2+2n+1,
∴n2+[n(n+1)]2+(n+1)2=[n(n+1)+1]2.
点评 此题考查因式分解的实际运用,掌握完全平方公式是解决问题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
15.某种商品的进价为a元,商店将价格提高50%后作为零售价销售,在销售旺季过后,商店又以7折的价格开展促销活动,这时,一件商品的促销价格为( )
| A. | a元 | B. | 0.7a元 | C. | 1.05a元 | D. | 0.93a元 |
2.在Rt△ABC中,如果三边长度都扩大2倍,则锐角A的余切值( )
| A. | 缩小2倍 | B. | 扩大2倍 | C. | 不变 | D. | 不能确定 |
16.在数轴上点A表示的数是-2,点B到点A的距离是4,则点表示是( )
| A. | 6 | B. | -2 | C. | -6 | D. | -6或2 |
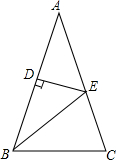 如图,△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点.
如图,△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点.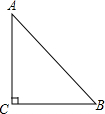 如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.
如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.