题目内容
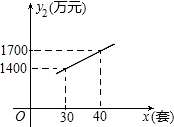 已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套,已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套,已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.(1)直接写出y2与x之间的函数关系式,并求月产量x的取值范围;
(2)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)设函数关系式为y2=kx+b,把(30,1400)(40,1700)代入求解即可;根据题中条件“每套产品的生产成本不高于50万元,每套产品的售价不低于90万元”列出不等式组求解月产量x的范围;
(2)根据等量关系“设备的利润=每台的售价×月产量-生产总成本”列出函数关系式求得最大值.
(2)根据等量关系“设备的利润=每台的售价×月产量-生产总成本”列出函数关系式求得最大值.
解答:解:(1)设函数关系式为y2=kx+b,把坐标(30,1400)(40,1700)代入,
解得:
,
∴函数关系式y2=30x+500;
依题意得:
,
解得:25≤x≤40;
(2)∵W=x•y1-y2=x(170-2x)-(500+30x)=-2x2+140x-500
∴W=-2(x-35)2+1950
∵25<35<40,
∴当x=35时,W最大=1950.
答:当月产量为35件时,利润最大,最大利润是1950万元.
|
解得:
|
∴函数关系式y2=30x+500;
依题意得:
|
解得:25≤x≤40;
(2)∵W=x•y1-y2=x(170-2x)-(500+30x)=-2x2+140x-500
∴W=-2(x-35)2+1950
∵25<35<40,
∴当x=35时,W最大=1950.
答:当月产量为35件时,利润最大,最大利润是1950万元.
点评:本题考查了二次函数的应用及待定系数法求函数解析式,难点在第二问,要求我们熟练运用配方法求二次函数的最值,另外要结合实际,考虑是否能取到最小.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
下列各数中,相反数是-2的是( )
| A、|-2| | ||
| B、-|-2| | ||
C、
| ||
D、-
|