题目内容
如图,抛物线y=-x2+bx+c经过A(-1,0),C(0,4)两点,与x轴交于另一点B,
(1)求抛物线的解析式;
(2)求P在第一象限的抛物线上,P点的横坐标为t,过点P向x轴做垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式并求出m的最大值;
(3)在(2)的条件下,抛物线上一点D的纵坐标为m的最大值,连接BD,在抛物线是否存在点E(不与点A,B,C重合)使得∠DBE=45°?若不存在.请说明理由;若存在请求E点的坐标.
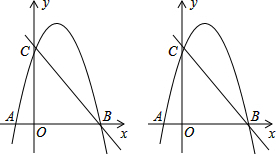
(1)求抛物线的解析式;
(2)求P在第一象限的抛物线上,P点的横坐标为t,过点P向x轴做垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式并求出m的最大值;
(3)在(2)的条件下,抛物线上一点D的纵坐标为m的最大值,连接BD,在抛物线是否存在点E(不与点A,B,C重合)使得∠DBE=45°?若不存在.请说明理由;若存在请求E点的坐标.
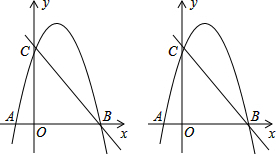
考点:二次函数综合题
专题:
分析:(1)把点A、B的坐标代入抛物线解析式,解关于b、c的方程组求出b、c的值即可得到抛物线解析式,令y=0,解关于x的一元二次方程即可得到点C的坐标;
(2)根据抛物线的解析式y=-x2+3x+4,令y=0求得点B的坐标为(4.0),设直线BC的解析式为y=kx+a
把点B、C的坐标代入直线BC的解析式为y=kx+a,解关于k、a的方程组求出k、a的值,所以直线BC的解析式为y=-x+4,设P点的坐标为(t,-t2+3t+4),则Q点的坐标为(t,-t+4),所以m=(-t2+3t+4)-(-t+4),整理得m=-(t-2)2+4,根据关于m、t的二次函数即可求得.
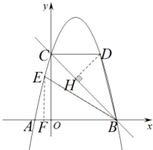
(3)根据m的最大值是4,代入y=-x2+3x+4,可求得D点的坐标(3,4),过D点作DH⊥BC,过E点作EF⊥x轴,由OC=OB=4得△DCB为等腰直角三角形,从而得出△CDH为等腰直角三角形,通过等腰直角三角形求得CN、BH的值,然后根据三角形相似求得EF、BF的关系,设出E点的坐标,然后代入y=-x2+3x+4即可求得.
(2)根据抛物线的解析式y=-x2+3x+4,令y=0求得点B的坐标为(4.0),设直线BC的解析式为y=kx+a
把点B、C的坐标代入直线BC的解析式为y=kx+a,解关于k、a的方程组求出k、a的值,所以直线BC的解析式为y=-x+4,设P点的坐标为(t,-t2+3t+4),则Q点的坐标为(t,-t+4),所以m=(-t2+3t+4)-(-t+4),整理得m=-(t-2)2+4,根据关于m、t的二次函数即可求得.
(3)根据m的最大值是4,代入y=-x2+3x+4,可求得D点的坐标(3,4),过D点作DH⊥BC,过E点作EF⊥x轴,由OC=OB=4得△DCB为等腰直角三角形,从而得出△CDH为等腰直角三角形,通过等腰直角三角形求得CN、BH的值,然后根据三角形相似求得EF、BF的关系,设出E点的坐标,然后代入y=-x2+3x+4即可求得.
解答:解:(1)抛物线y=-x2+bx+c经过A(-1,0)、C(0,4)两点,
∴
解得
∴抛物线的解析式y=-x2+3x+4
(2)令-x2+3x+4=0,
解得x1=-1,x2=4,
∴B(4,0)
设直线BC的解析式为y=kx+a
∴
解得
,
∴直线BC的解析式为y=-x+4
设P点的坐标为(t,-t2+3t+4),则Q点的坐标为(t,-t+4)
∴m=(-t2+3t+4)-(-t+4)=-(t-2)2+4
整理得m=-(t-2)2+4,
∴当t=2时,m的最大值为4
(3)存在
∵抛物线一点D的纵坐标为m的最大值4,
∴-x2+3x+4=4,解得x1=0(舍),x2=3
∴D(3,4),CD=3
∵C(0,4),
∴CD∥x轴,
∵OC=OB=4,
∴△BOC为直角三角形,
过点D作DH⊥BC于H,过点E作EF⊥x于点F,在△CDB中,CD=3,∠DCB=45°
∴CH=DH=
,
∵CB=4
,∴BH=CB-CH=
∵∠DBE=∠CBO=45°
∴∠DBE-∠CBE=∠CBO-∠CBE,
即∠DBC=∠EBF
∴tan∠DBC=
=
=
设EF=3a∴BF=5a
∴OF=5a-4
∴F(4-5a,0),E(4-5a,3a)
∵点E在抛物线上
∴3a=-(4-5a)2+3(4-5a)+4
解得a1=0 a2=
∴E(-
,
).
∴
|
解得
|
∴抛物线的解析式y=-x2+3x+4
(2)令-x2+3x+4=0,
解得x1=-1,x2=4,
∴B(4,0)
设直线BC的解析式为y=kx+a
∴
|
解得
|
∴直线BC的解析式为y=-x+4
设P点的坐标为(t,-t2+3t+4),则Q点的坐标为(t,-t+4)
∴m=(-t2+3t+4)-(-t+4)=-(t-2)2+4
整理得m=-(t-2)2+4,
∴当t=2时,m的最大值为4
(3)存在
∵抛物线一点D的纵坐标为m的最大值4,
∴-x2+3x+4=4,解得x1=0(舍),x2=3
∴D(3,4),CD=3
∵C(0,4),
∴CD∥x轴,
∵OC=OB=4,
∴△BOC为直角三角形,
过点D作DH⊥BC于H,过点E作EF⊥x于点F,在△CDB中,CD=3,∠DCB=45°
∴CH=DH=
3
| ||
| 2 |
∵CB=4
| 2 |
5
| ||
| 2 |
∵∠DBE=∠CBO=45°
∴∠DBE-∠CBE=∠CBO-∠CBE,
即∠DBC=∠EBF
∴tan∠DBC=
| DH |
| HB |
| EF |
| BF |
| 3 |
| 5 |
设EF=3a∴BF=5a
∴OF=5a-4
∴F(4-5a,0),E(4-5a,3a)
∵点E在抛物线上
∴3a=-(4-5a)2+3(4-5a)+4
解得a1=0 a2=
| 22 |
| 25 |
∴E(-
| 2 |
| 5 |
| 66 |
| 25 |

点评:本题是对二次函数的综合考查,主要应用了待定系数法求函数解析式,抛物线与x轴的交点问题,以及三角函数的问题.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目

 如图,二次函数图象过点M(2,0),直线AB与该二次函数的图象交于A(0,2)、B(6,8)两点.
如图,二次函数图象过点M(2,0),直线AB与该二次函数的图象交于A(0,2)、B(6,8)两点. 如图,矩形BC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3).双曲线
如图,矩形BC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3).双曲线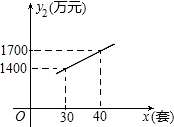 已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套,已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套,已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.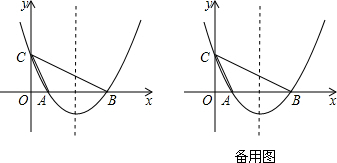

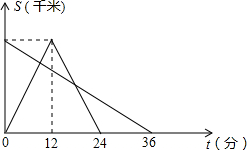 甲、乙两车同时分别从A、B两地出发相向而行,甲车到达B地后立即返回A地,若两车离A地的距离S(千米)与所用时间t(分)的函数关系如图,则甲、乙两车在途中两次相遇的间隔时间为
甲、乙两车同时分别从A、B两地出发相向而行,甲车到达B地后立即返回A地,若两车离A地的距离S(千米)与所用时间t(分)的函数关系如图,则甲、乙两车在途中两次相遇的间隔时间为