题目内容
解不等式组：
，并把其解集在数轴上表示出来．
|
考点：解一元一次不等式组,在数轴上表示不等式的解集
专题：
分析：先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集表示在数轴上即可．
解答：解：
，
解①得：x≤2，
解②得：x＞-1，
，
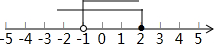不等式组的解集是：-1＜x≤2．
|
解①得：x≤2，
解②得：x＞-1，
，不等式组的解集是：-1＜x≤2．
点评：本题主要考查了一元一次不等式组的解法，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．
练习册系列答案
相关题目
某人帐户现存款a元，每月支出b元，收入c元（a、b、c都是常数且大于0），则帐户余额（不计利息）与月份的函数图象可能是下图中的（ ）
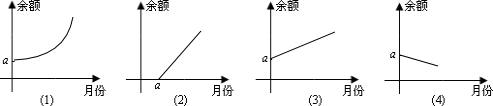
| A、（1）（3） |
| B、（3）（4） |
| C、（1）（3）（4） |
| D、（2）（3）（4） |
已知整数x满足是不等式组
，则x的算术平方根为（ ）
|
| A、2 | ||
| B、±2 | ||
C、
| ||
| D、4 |
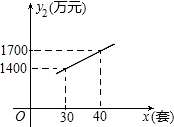已知某种高新技术设备的生产成本不高于50万元/套，售价不低于90万元/套，已知这种设备的月产量x（套）与每套的售价y1（万元）之间满足关系式y1=170-2x，月产量x（套）与生产总成本y2（万元）存在如图所示的函数关系．
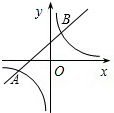如图，已知一次函数与反比例函数的图象交于点A（-3，-1）和B（a，3）．
