题目内容
如图①有两块大小不同的等腰直角三角板△ABC和△DCE,连接AD,BE,则:
(1)AD和BE的关系是 (位置关系和数量关系);
(2)如图②,若△DCE绕点C顺时针旋转90°,(1)中的结论是否成立 ;
(3)若△DCE绕点C顺时针旋转,①当0°<α<90°时,②当90°<α<180°时,分别画出两种情况下的图形,(1)中结论是否改变 ,选择一种情况加以证明.

(1)AD和BE的关系是
(2)如图②,若△DCE绕点C顺时针旋转90°,(1)中的结论是否成立
(3)若△DCE绕点C顺时针旋转,①当0°<α<90°时,②当90°<α<180°时,分别画出两种情况下的图形,(1)中结论是否改变
考点:旋转的性质,全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据等腰三角形性质推出∠ACB=∠DCE=90°,AC=BC,CD=CE,根据SAS证明两三角形全等即可;根据全等推出∠DAC=∠EBC,求出∠DAC+∠ADC=90°,推出∠CBE+∠BDF=90°,求出∠BFD=90°即可.
(2)根据等腰直角三角形的性质,等量代换即可证得.
(3)画出图形,结合图形证明三角形全等证得.
(2)根据等腰直角三角形的性质,等量代换即可证得.
(3)画出图形,结合图形证明三角形全等证得.
解答:答(1)相等且垂直.
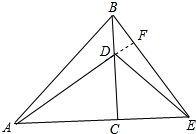 证明:延长AD交BE于F,
证明:延长AD交BE于F,
∵等腰直角三角形ACB和△DCE,
∴∠ACB=∠DCE=90°,AC=BC,CD=CE,
在△ADC和△BEC中,
∴△ADC≌△BEC(SAS).
∴AD=BE
由(1)知:△ADC≌△BEC,
∴∠DAC=∠EBC,
∵∠ACD=90°,
∴∠DAC+∠ADC=90°,
∵∠BDF=∠ADC,
∴∠EBC+∠BDF=90°,
∴∠BFD=180°-(∠EBC+∠BDF)=90°,
∴AD⊥BE.
(2)成立.
证明:∵等腰直角三角形ACB和△DCE,
∴BC=AC CD=CE
根据旋转的性质得
∠BCD=90°
∴AD⊥BE
∴BC+CE=AC+CD
即AD=BE
∴AD和BE垂直且相等仍然成立.
(3)①不变,如图: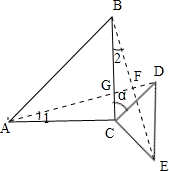
连接BE和AD
在△BCE和△ACD中,
∵BC=AC,∠BCE=90°+α,∠ACD=90°+α,
∴∠ACD=∠BCE
CE=CD,
∴△BCE≌△ACD
∴BE=AD,∠1=∠2
∵∠1+∠AGC=90°
∴∠2+∠AGC=90°,
∴∠AFG=90°.
即BE⊥AD.
 证明:延长AD交BE于F,
证明:延长AD交BE于F,∵等腰直角三角形ACB和△DCE,
∴∠ACB=∠DCE=90°,AC=BC,CD=CE,
在△ADC和△BEC中,
|
∴△ADC≌△BEC(SAS).
∴AD=BE
由(1)知:△ADC≌△BEC,
∴∠DAC=∠EBC,
∵∠ACD=90°,
∴∠DAC+∠ADC=90°,
∵∠BDF=∠ADC,
∴∠EBC+∠BDF=90°,
∴∠BFD=180°-(∠EBC+∠BDF)=90°,
∴AD⊥BE.
(2)成立.
证明:∵等腰直角三角形ACB和△DCE,
∴BC=AC CD=CE
根据旋转的性质得
∠BCD=90°
∴AD⊥BE
∴BC+CE=AC+CD
即AD=BE
∴AD和BE垂直且相等仍然成立.
(3)①不变,如图:

连接BE和AD
在△BCE和△ACD中,
∵BC=AC,∠BCE=90°+α,∠ACD=90°+α,
∴∠ACD=∠BCE
CE=CD,
∴△BCE≌△ACD
∴BE=AD,∠1=∠2
∵∠1+∠AGC=90°
∴∠2+∠AGC=90°,
∴∠AFG=90°.
即BE⊥AD.
点评:本题考查了等腰直角三角形性质,全等三角形的性质和判定,三角形的内角和定理等知识点,主要考查学生运用定理进行推理的能力.熟练运用旋转的性质,全等三角形的判断与性质,锐角三角函数值等知识点进行解答即可

练习册系列答案
相关题目
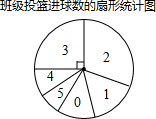 小华班上比赛投篮,每人5次,如图是班上所有学生的投篮进球数的扇形统计图,则下列关于班上所有学生投进球数的统计量正确的是( )
小华班上比赛投篮,每人5次,如图是班上所有学生的投篮进球数的扇形统计图,则下列关于班上所有学生投进球数的统计量正确的是( )| A、中位数是3个 |
| B、中位数是2.5个 |
| C、众数是2个 |
| D、众数是5个 |
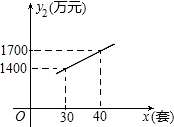 已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套,已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套,已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.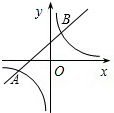 如图,已知一次函数与反比例函数的图象交于点A(-3,-1)和B(a,3).
如图,已知一次函数与反比例函数的图象交于点A(-3,-1)和B(a,3).