题目内容
17. 如图,直角梯形ABCD的中位线EF=4,垂直于底的腰AB=5,则图中阴影部分的面积是10.
如图,直角梯形ABCD的中位线EF=4,垂直于底的腰AB=5,则图中阴影部分的面积是10.
分析 过D作DM⊥EF于M,过C作CN⊥EF于N,根据梯形的中位线求出EF∥AD,求出四边形AEMD和四边形BENC都是矩形,根据矩形的性质得出DM=AE,CN=BE,求出DM+CN=AB=5,根据面积公式求出即可.
解答 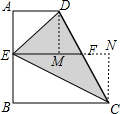
解:过D作DM⊥EF于M,过C作CN⊥EF于N,
∵梯形ABCD是直角梯形,EF为梯形的中位线,
∴EF∥AD,
∴∠A=∠AEM═∠DME=90°,∠B=∠CNE=∠BEF=90°,
∴四边形AEMD和四边形BENC都是矩形,
∴DM=AE,CN=BE,
∴DM+CN=AB=5,
∵直角梯形ABCD的中位线EF=4,
∴图中阴影部分的面积S=$\frac{1}{2}$×EF×(DM+CN)=$\frac{1}{2}$×4×5=10,
故答案为:10.
点评 本题考查了矩形的性质和判定,三角形的面积,梯形的性质的应用,能求出DM+CN=AB=5是解此题的关键,注意:梯形的中位线平行于两底,并且等于两底和的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若二次函数y=ax2+$\sqrt{2}$(a≠0),当x分别取x1,x2时,函数值相等,则当x取x1+x2时,函数值为( )
| A. | 0 | B. | a | C. | $\sqrt{2}$ | D. | 不确定 |
9.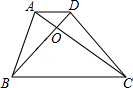 如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )
如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )
 如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )
如图,梯形ABCD的对角线AC、BD相交于O,若AD=3,BC=9,则AO:OC=( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 11:20 |
6.要反映某种股票的涨跌情况,最好选择( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 列表 |
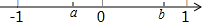 实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.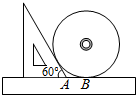 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是3$\sqrt{3}$cm.
如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是3$\sqrt{3}$cm.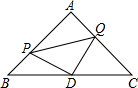 如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.
如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.