题目内容
9．
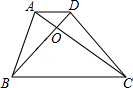如图，梯形ABCD的对角线AC、BD相交于O，若AD=3，BC=9，则AO：OC=（ ）| A． | 1：2 | B． | 1：3 | C． | 2：3 | D． | 11：20 |
分析 由梯形的性质得AD∥BC，则可判断△AOD∽△COB，然后利用相似比即可得到AO：OC的值．
解答 解：∵四边形ABCD为梯形，
∴AD∥BC，
∴△AOD∽△COB，
∴$\frac{AO}{OC}$=$\frac{AD}{BC}$=$\frac{3}{9}$=$\frac{1}{3}$．
故选B．
点评 本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．也考查了梯形的性质．
练习册系列答案
相关题目
如图，直角梯形ABCD的中位线EF=4，垂直于底的腰AB=5，则图中阴影部分的面积是10．