Question

5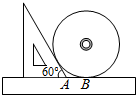．如图，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB=3cm，则此光盘的半径是3$\sqrt{3}$cm．

Answer 1

分析 连接OA，根据题意求出∠OAB=60°，再根据直角三角形的性质和勾股定理求得OB，从而得出光盘的直径．

解答 解：连接OA，
∵∠CAD=60°，
∴∠CAB=120°，
∵AB和AC与⊙O相切，
∴∠OAB=∠OAC，
∴∠OAB=$\frac{1}{2}$∠CAB=60°
∵AB=3cm，
∴OA=6cm，
∴由勾股定理得OB=3$\sqrt{3}$cm，
∴光盘的半径是3$\sqrt{3}$cm．
故答案为：3$\sqrt{3}$．

点评 此题考查了切线的性质，切线长定理，含30°直角三角形的性质，以及勾股定理，熟练掌握切线的性质是解本题的关键．