题目内容
2．△ABC中，∠C为锐角，BC=7，cosB=$\frac{\sqrt{2}}{2}$，sinC=$\frac{3}{5}$，则△ABC的面积是10.5．分析 直接利用特殊角的三角函数值得出∠B的度数，再利用锐角三角函数关系表示出AD，BD，DC的长，进而得出答案．
解答 
解：如图所示：∵cosB=$\frac{\sqrt{2}}{2}$，
∴∠B=45°，
∵sinC=$\frac{3}{5}$，
∴设AD=3x，则AC=5x，DC=4x，BD=3x，
∵BC=7，
∴BD+DC=3x+4x=7x=7，
解得：x=1，
故AD=3，
则△ABC的面积是：$\frac{1}{2}$×3×7=10.5．
故答案为：10.5．
点评 此题主要考查了特殊角的三角函数值以及三角形面积求法，正确表示出AD，BD，DC的长是解题关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
如图是著名的赵爽弦图，它是由四个全等的直角三角形拼成，每个直角三角形的两直角边的长分别为a和b，斜边长为c，请你用它来验证勾股定理．
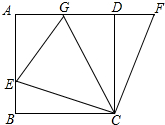如图，在正方形ABCD中，点E在AB上，F是AD延长线上一点，且DF=BE，点G在AD上，且∠ECG=45°．