题目内容
14.如图①,在△ABC中,D、E分别是AB、AC上的点,AB=AC,AD=AE,然后将△ADE绕点A顺时针旋转一定角度,连接BD,CE,得到图②,将BD、CE分别延长至M、N,使DM=$\frac{1}{2}$BD,EN=$\frac{1}{2}$CE,得到图③,请解答下列问题: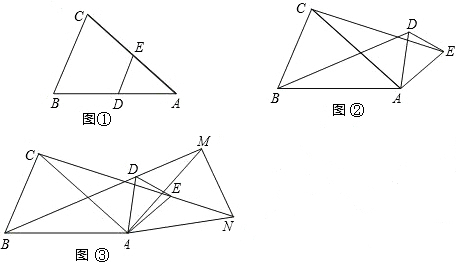
(1)在图②中,BD与CE的数量关系是BD=CE;
(2)在图③中,判断△AMN的形状,及∠MAN与∠BAC的数量关系,并证明你的猜想.
分析 (1)由旋转的性质知∠BAD=∠CAE,证△BAD≌△CAE可得;
(2)由△BAD≌△CAE知∠ABD=∠ACE,BD=CE,结合DM=$\frac{1}{2}$BD,EN=$\frac{1}{2}$CE可得BM=CN,再证△ABM≌△ACN得AM=AN,∠BAM=∠CAN,即可得证.
解答 解:(1)由旋转的性质知∠BAD=∠CAE,
在△BAD和△CAE中,
∵$\left\{\begin{array}{l}{BA=CA}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴BD=CE,
故答案为:BD=CE;
(2)AM=AN,∠MAN=∠BAC,
由(1)知△BAD≌△CAE,
∴∠ABD=∠ACE,BD=CE,
又∵DM=$\frac{1}{2}$BD,EN=$\frac{1}{2}$CE,
∴BM=CN,
在△ABM和△ACN中,
∵$\left\{\begin{array}{l}{BM=CN}\\{∠ABM=∠ACN}\\{BA=CA}\end{array}\right.$,
∴△ABM≌△ACN(SAS),
∴AM=AN,∠BAM=∠CAN,即∠BAC+∠CAM=∠CAM+∠MAN,
∴△AMN为等腰三角形,且∠MAN=∠BAC.
点评 本题主要考查旋转的性质和全等三角形的判定与性质,根据所求证确定所需求证的三角形全等是解题的关键.

练习册系列答案
相关题目
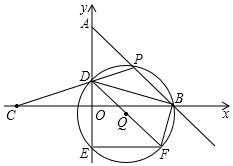 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(-4,0),点P在线段AB上运动,连结CP与y轴交于点D,连结BD.过P、D、B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF、BF.
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(-4,0),点P在线段AB上运动,连结CP与y轴交于点D,连结BD.过P、D、B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF、BF.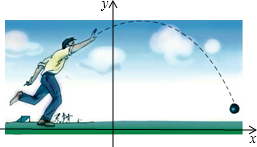 如图,男生张波推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系用如图所示的二次函数图象表示,该二次函数满足y=a(x-4)2+h.他的出手高度为$\frac{5}{3}$m时,铅球推出的距离是10m,
如图,男生张波推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系用如图所示的二次函数图象表示,该二次函数满足y=a(x-4)2+h.他的出手高度为$\frac{5}{3}$m时,铅球推出的距离是10m, 如图,在Rt△ABC,∠C=90°,AB=10,BC=8,则AC=6.
如图,在Rt△ABC,∠C=90°,AB=10,BC=8,则AC=6.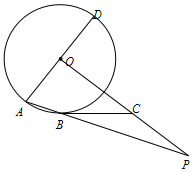 如图,AD是⊙O的直径,AB为⊙O 的弦,BC与⊙O相切,B为切点,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
如图,AD是⊙O的直径,AB为⊙O 的弦,BC与⊙O相切,B为切点,OP与AB的延长线交于点P.点C在OP上,且BC=PC.