题目内容
11.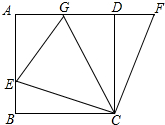 如图,在正方形ABCD中,点E在AB上,F是AD延长线上一点,且DF=BE,点G在AD上,且∠ECG=45°.
如图,在正方形ABCD中,点E在AB上,F是AD延长线上一点,且DF=BE,点G在AD上,且∠ECG=45°.(1)观察图形,结合已知条件试找出图中的全等三角形,并说明你是如何推理出来的.
(2)GE、BE、DG的关系怎样,为什么?
分析 (1)先利用“ASA”证明△BCE≌△DCG,则CE=CF,∠BCE=∠DCF,再证明∠GCF=∠ECG=45°,然后根据“SAS”证明△ECG≌△FCG;
(2)利用△ECG≌△FCG得到EG=GF,所以GE=GD+DF=BE+DG.
解答 解:(1)∵四边形ABCD为正方形,
∴CB=CD,∠B=∠ADC=∠BCD=90°,
在△BCE和△DCG中
$\left\{\begin{array}{l}{BE=DF}\\{∠B=∠CDF}\\{CB=CD}\end{array}\right.$,
∴△BCE≌△DCG(SAS);
∴CE=CF,∠BCE=∠DCF,
∵∠BCE+∠ECD=90°,
∴∠ECD+∠DCF=90°,即∠ECF=90°,
∵∠ECG=45°,
∴∠GCF=∠ECG=45°,
在△ECG和△FCG中
$\left\{\begin{array}{l}{CE=CF}\\{∠GCE=∠GCF}\\{CG=CG}\end{array}\right.$,
∴△ECG≌△FCG(SAS);
(2)∵△ECG≌△FCG,
∴EG=GF,
∴GE=GD+DF,
而DF=BE,
∴GE=BE+DG.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角.也考查了全等三角形的判定与性质.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
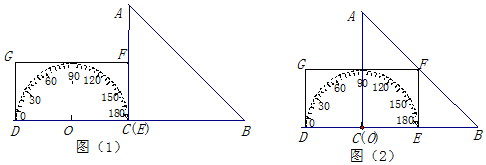
 如图,在Rt△ABC,∠C=90°,AB=10,BC=8,则AC=6.
如图,在Rt△ABC,∠C=90°,AB=10,BC=8,则AC=6.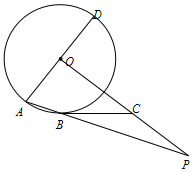 如图,AD是⊙O的直径,AB为⊙O 的弦,BC与⊙O相切,B为切点,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
如图,AD是⊙O的直径,AB为⊙O 的弦,BC与⊙O相切,B为切点,OP与AB的延长线交于点P.点C在OP上,且BC=PC.