题目内容
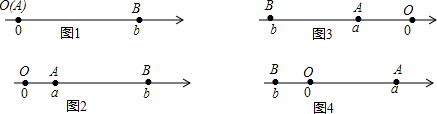
12.(1)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时,①如图2,点A、B都在原点的右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(-b)=|a-b|;
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是3,数轴上表示-2和-5的两点之间的距离是3;数轴上表示1和-3的两点之间的距离是4;
②数轴上表示x和-1的两点A和B之间的距离是|x|+1;
③如果|x+3|=2,那么x为-1或-5;
④代数式|x+3|+|x-2|最小值是5,当代数式|x+3|+|x-2|取最小值时,相应的x的取值范围是-3≤x≤2.
分析 由所给阅读材料可知两点间的距离即为数轴上右边的点所对应的数减去左边的点所对应的数,据此分别求解即可.
解答 解:
①|5-2|=5-2=3,|-2-(-5)|=-2-(-5)=-2+5=3,|1-(-3)|=1-(-3)=1+3=4,
故答案为:3;3;4;
②由题意可知|x-(-1)|=|x|+1,
故答案为:|x|+1;
③由题意可知x+3=2或x+3=-2,解得x=-1或x=-5,
故答案为:-1或-5;
④由绝对值的意义可知当-3≤x≤2时,|x+3|+|x-2的值即为2与-3两点间的距离,此时最小,最小值为|2-(-3)|=5,
故答案为:5;-3≤x≤2.
点评 本题主要考查绝对值的意义,由所给阅读材料得出两点间的距离即为数轴上对应两点的数的差的绝对值是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
20.甲、乙两名队员参加射击训练,成绩分别被制成如图两个统计图:
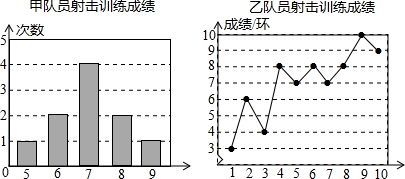
根据以上信息,整理分析数据如表:
(1)写出表格中a,b,c的值:a=7,b=7.5,c=1.2;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?

根据以上信息,整理分析数据如表:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | c |
| 乙 | 7 | b | 8 | 4.2 |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
 已知:如图,在边长为8的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
已知:如图,在边长为8的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.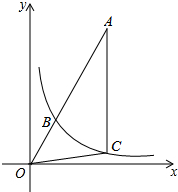 反比例函数y=$\frac{k}{x}$ (x>0)的图象如图,点B在图象上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交y=$\frac{k}{x}$(x>0)的图象于点C,连接OC,S△AOC=5,求k值.
反比例函数y=$\frac{k}{x}$ (x>0)的图象如图,点B在图象上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交y=$\frac{k}{x}$(x>0)的图象于点C,连接OC,S△AOC=5,求k值. 如图,在△ABC中,点D是边BC上一点,∠1=∠B,∠2=∠C,∠BAC=63°,求∠DAC的度数.
如图,在△ABC中,点D是边BC上一点,∠1=∠B,∠2=∠C,∠BAC=63°,求∠DAC的度数. (1)计算:(3-π)0+2tan60°+(-1)2015-$\sqrt{12}$.
(1)计算:(3-π)0+2tan60°+(-1)2015-$\sqrt{12}$.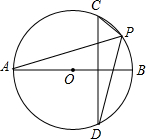 如图AB是⊙O的直径,CD是⊙O的弦,CD垂直AB,P是弧CD上的一点(不与C、D重合),∠APC与∠APD相等吗?为什么?
如图AB是⊙O的直径,CD是⊙O的弦,CD垂直AB,P是弧CD上的一点(不与C、D重合),∠APC与∠APD相等吗?为什么?