题目内容
20.甲、乙两名队员参加射击训练,成绩分别被制成如图两个统计图: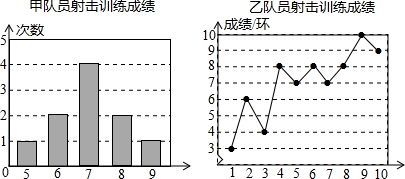
根据以上信息,整理分析数据如表:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | c |
| 乙 | 7 | b | 8 | 4.2 |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
分析 (1)利用平均数的计算公式直接计算平均分即可;将乙的成绩从小到大重新排列,用中位数的定义直接写出中位数即可;根据甲的平均数利用方差的公式计算即可;
(2)结合平均数和中位数、众数、方差三方面的特点进行分析.
解答 解:(1)甲的平均成绩a=$\frac{5×1+6×2+7×4+8×2+9×1}{1+2+4+2+1}$=7(环),
∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b=$\frac{7+8}{2}$=7.5(环),
其方差c=$\frac{1}{10}$×[(5-7)2+2(6-7)2+4(7-7)2+2×(8-7)2+(9-7)2]=1.2(环);
故答案为:7,7.5,1.2;
(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定;
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
点评 本题考查的是条形统计图和方差、平均数、中位数、众数的综合运用.熟练掌握平均数的计算,理解方差的概念,能够根据计算的数据进行综合分析.

练习册系列答案
相关题目
 表示a+b-c,例如
表示a+b-c,例如 是5+4-6,那么
是5+4-6,那么 +
+ 是2y+z.
是2y+z.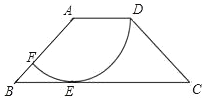 如图,在四边形ABCD中,AD∥BC,AD=2,AB=2$\sqrt{2}$,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
如图,在四边形ABCD中,AD∥BC,AD=2,AB=2$\sqrt{2}$,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.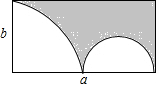 从长与宽分别为a与b的长方形中挖去一个四分之一圆和一个半圆,如图所示,用式子表示剩余部分的面积,并说明该式子是否为多项式.
从长与宽分别为a与b的长方形中挖去一个四分之一圆和一个半圆,如图所示,用式子表示剩余部分的面积,并说明该式子是否为多项式.