题目内容
4．
如图，在△ABC中，点D是边BC上一点，∠1=∠B，∠2=∠C，∠BAC=63°，求∠DAC的度数．
分析 通过∠3与∠2的关系以及内角和定理解出∠2，即∠1的大小，进而可求∠DAC．
解答 解：∵∠2=∠1+∠B，∠2=∠C，∠1=∠B，∠BAC=63°
∴∠4=∠1+∠2=2∠2，
∵∠BAC+∠B+∠C=180°，
即3∠B+63°=180°，
∴∠B=39°，
∠DAC=∠BAC-∠1=63°-39°=24°．
点评 本题主要考查了三角形的内角和定理及外角的性质，难度适中．
练习册系列答案
相关题目
15．
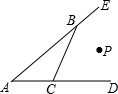如图，①点P在∠BAC的平分线上；②点P在∠CBE的平分线上；③点P在∠BCD的平分线上，三条中满足什么条件，得点P到△ABC三条边距离相等（ ）
如图，①点P在∠BAC的平分线上；②点P在∠CBE的平分线上；③点P在∠BCD的平分线上，三条中满足什么条件，得点P到△ABC三条边距离相等（ ）| A． | ① | B． | ② | C． | ③ | D． | ①②或①③或②③ |
19．
如图，D为∠ABC的平分线上一点，P为平分线上异于D的一点，PA⊥BA，PC⊥BC，垂足分别为A、C，则下列结论错误的是（ ）
如图，D为∠ABC的平分线上一点，P为平分线上异于D的一点，PA⊥BA，PC⊥BC，垂足分别为A、C，则下列结论错误的是（ ）| A． | AD=CD | B． | ∠DAP=∠DCP | C． | ∠ADB=∠BDC | D． | PD=BD |
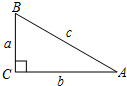在Rt△ABC中，若∠C=90°，a=5，∠A=30°，求∠B、b、c．