��Ŀ����
3������⣺�¶��壺�ԷǸ�ʵ��x���������롰����λ��ֵ��Ϊ��x����������nΪ�Ǹ�����ʱ�����$n-\frac{1}{2}��x��n+\frac{1}{2}����x��=n$�����磼0��=��0.48��=0����0.64��=��1.49��=1����2��=2����3.5��=��4.12��=4�����Խ���������⣺
��1����գ�
�٣��У�=3����ΪԲ���ʣ�
�������x-1��=3����ʵ��x��ȡֵ��ΧΪ3.5��x��4.5
��д��һ��x��yֵ��ʹ��ʽ��x+y��=��x��+��y�������������磺x=0.6��y=0.7��дһ�鼴�ɣ�
��2����nΪ��������Ϊ������������$y={x^2}-x+\frac{1}{4}$���Ա���x���㣼x��=nʱ����Ӧ�ĺ���ֵyΪ�����ĸ�����Ϊa����a��ֵ����n��ʾ��
���� ��1���ٸ��ݣ�x���Ķ��弴�ɵó����ۣ�
�ڸ��ݣ�x�����壬�ɣ�x-1��=3�г����̼��ɽ����
�۾ٷ���˵�����ɣ�
��2���ɺ���y=x2-x+$\frac{1}{4}$=��x-$\frac{1}{2}$��2��nΪ�������֣�x��=n����n-$\frac{1}{2}$��x��n+$\frac{1}{2}$ʱ��y��x������������г�����ʽ�����ɽ�����⣮
��� �⣺��1����������ɵã����У�=3��
�ʴ�Ϊ��3��
�ڡߣ�x-1��=3��
��2.5��x-1��3.5
��3.5��x��4.5��
�ʴ�Ϊ��3.5��x��4.5��
�۾ٷ�������0.6��+��0.7��=1+1=2������0.6+0.7��=��1.3��=1��
�ࣼ0.6��+��0.7���٣�0.6+0.7����
�ࣼx+y��=��x��+��y����һ��������
�ʴ𰸷ֱ�Ϊ0.6��0.7��
��2�����ߺ���y=x2-x+$\frac{1}{4}$=��x-$\frac{1}{2}$��2��nΪ�������֣�x��=n
��n-$\frac{1}{2}$��x��n+$\frac{1}{2}$ʱ��y��x�����������
�ࣨn-1��2��y��n2��
��n2-2n+1��y��n2
��y������
��y=n2-2n+1��n2-2n+2��n2-2n+3������n2-2n+2n����2n-1��y��
��a=2n-1
���� ���⿼����κ����ۺ��⣬�������Ĺؼ������⣺�ԷǸ�ʵ��x���������롱����λ��ֵ��Ϊ��x����������nΪ�Ǹ�����ʱ�����n-$\frac{1}{2}$��x��n+$\frac{1}{2}$����x��=n��ѧ�������ת��Ϊ����ʽ�������п�������Ŀ��

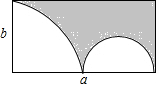 �ӳ�����ֱ�Ϊa��b�ij���������ȥһ���ķ�֮һԲ��һ����Բ����ͼ��ʾ����ʽ�ӱ�ʾʣ�ಿ�ֵ��������˵����ʽ���Ƿ�Ϊ����ʽ��
�ӳ�����ֱ�Ϊa��b�ij���������ȥһ���ķ�֮һԲ��һ����Բ����ͼ��ʾ����ʽ�ӱ�ʾʣ�ಿ�ֵ��������˵����ʽ���Ƿ�Ϊ����ʽ��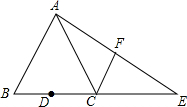 ��ͼ����֪�ڡ�ABC�У�AB=AC��tan��B=2��BC=4��DΪBC�ߵ��е㣬��E��BC�ߵ��ӳ����ϣ���CE=BC������AE��FΪ�߶�AE���е�
��ͼ����֪�ڡ�ABC�У�AB=AC��tan��B=2��BC=4��DΪBC�ߵ��е㣬��E��BC�ߵ��ӳ����ϣ���CE=BC������AE��FΪ�߶�AE���е�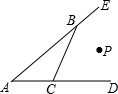 ��ͼ���ٵ�P�ڡ�BAC��ƽ�����ϣ��ڵ�P�ڡ�CBE��ƽ�����ϣ��۵�P�ڡ�BCD��ƽ�����ϣ�����������ʲô�������õ�P����ABC�����߾�����ȣ�������
��ͼ���ٵ�P�ڡ�BAC��ƽ�����ϣ��ڵ�P�ڡ�CBE��ƽ�����ϣ��۵�P�ڡ�BCD��ƽ�����ϣ�����������ʲô�������õ�P����ABC�����߾�����ȣ�������
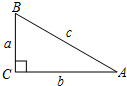 ��Rt��ABC�У�����C=90�㣬a=5����A=30�㣬���B��b��c��
��Rt��ABC�У�����C=90�㣬a=5����A=30�㣬���B��b��c��