题目内容
19.小王家距上班单位10km,某天他骑电动车去上班,走到路程的一半时发现忘带手机,此时离上班时间还有30分钟,于是他立刻骑电动车回家取手机,随后开车返回学校,已知小王开车到单位比他骑电动车到单位少用20分钟,且开车的平均速度是骑电动车速度的3倍,小王到家开门,取手机,启动车等共用了4分钟(除此之外不考虑其它因素)(1)求小王骑电动车的平均速度;
(2)请你判断小王能否按时上班,并说明理由.
分析 (1)设骑电动车速度为xkm/h,则开车的平均速度为3xkm/h,根据等量关系:小王开车到单位比他骑电动车到单位少用20分钟可得出方程,解出即可;
(2)计算出骑电动车、开车及回家取手机的时间和,然后与30比较即可作出判断.
解答 解:设骑电动车速度为xkm/h,则开车的平均速度为3xkm/h,可得:$\frac{10}{x}-\frac{10}{3x}=\frac{20}{60}$,
解得:x=20,
经检验x=20是原分式方程的解,且符合题意,
答:小王骑电动车的平均速度20km/h;
(2)小王回家的时间:$\frac{5}{20}=\frac{1}{4}$小时,开车到单位的时间:$\frac{10}{20×3}=\frac{1}{6}$小时,共用时间:$(\frac{1}{4}+\frac{1}{6})×60+4=29$分钟,因为29<30,
所以小王能按时上班.
点评 此题考查了分式方程的应用,设出骑电动车速度的速度,根据等量关系得出方程是解答本题的关键,注意分式方程一定要检验.

练习册系列答案
相关题目
14.某工厂现在平均每天比原计划多生产10台机器,现在生产700台机器所需时间与原计划生产500台机器所需时间相同,设原计划平均每天生产x台机器,根据题意列方程得( )
| A. | $\frac{700}{x}$=$\frac{500}{x+10}$ | B. | $\frac{700}{x-10}$=$\frac{500}{x}$ | C. | $\frac{700}{x}$=$\frac{500}{x-10}$ | D. | $\frac{700}{x+10}$=$\frac{500}{x}$ |
11.某市为提倡节约用水,采取分段收费.若每户每月用水不超过20m3,每立方米收费2元;若用水超过20m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水( )m3.
| A. | 38 | B. | 34 | C. | 28 | D. | 44 |
8.下列说法中正确的是( )
| A. | 无理数是无限不循环小数 | B. | 无限小数都是无理数 | ||
| C. | -1的平方根是±1 | D. | -3是9的算术平方根 |
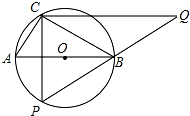 如图,Rt△ABC中,AB=10,AC:BC=3:4,以斜边AB为直径作⊙O,动点P在直径下方的半圆AB上运动(不与A、B重合),过点C作CQ⊥CP,与PB的延长线交于点Q.
如图,Rt△ABC中,AB=10,AC:BC=3:4,以斜边AB为直径作⊙O,动点P在直径下方的半圆AB上运动(不与A、B重合),过点C作CQ⊥CP,与PB的延长线交于点Q.