题目内容
7.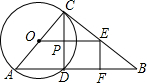 已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )
已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )| A. | OE∥AB | B. | BC=2DE | C. | AC•DF=DE•CD | D. | DE=$\sqrt{2}$PD |
分析 证明BC是⊙O的切线,进而得到P是CD的中点,利用中位线定理求出OE∥AB,据此判断A正确;证明E是BC的中点,利用∠CDB是直角,据此得到BC=2DE,判断B选项正确;证明△ACD∽△EDF,即可得到AC•DF=DE•CD,判断C选项正确;只有当PE=PD时DE才等于$\sqrt{2}$PD,据此判断D选项错误.
解答 解:∵∠ACB=90°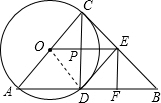 ,
,
∴BC是⊙O的切线,
∵BC是⊙O的切线,
∴OE垂直平分CD,∠OEC=∠OED,
∴P是CD的中点,
∴OP∥AB,
∴OE∥AB,
A选项正确,
∵OE∥AB,O是AC的中点,
∴E是BC的中点,
∵AC是直径,
∴∠ADC=90°,
∴CD⊥AB,
∴∠CDB=90°,
∴BC=2DE,
B选项正确;
∵EF⊥AB,
∴∠DFE=∠ADC=90°,
∵DE=CD,BC是⊙O的切线,
∴DE是⊙O的切线,
∴∠EDF=∠CAD,
∴△ACD∽△EDF
∴$\frac{AC}{DE}=\frac{CD}{DF}$,
∴AC•DF=DE•CD,
C选项正确.
在四边形PDFE中,我们可以证明它是矩形,而不具备证明它是正方形的条件,
∴DE=$\sqrt{P{E}^{2}+P{D}^{2}}$,
只有PE=PD时DE才等于$\sqrt{2}$PD,
D选项错误,
故选D.
点评 本题考查了圆的切线的性质、圆周角定理,相似三角形的判定与性质,切线长性质及三角形的中位线的运用,解答本题的关键是熟练掌握切线的判定定理以及切线的性质,此题有一定的难度.

练习册系列答案
相关题目
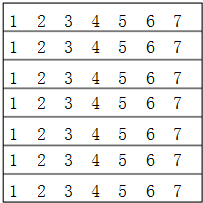 有七张相同的纸条,恰好组成一个正方形,每张纸条上都依次写上1~7这七个数字,现在要把这些字条剪短后,左右对调(不能上下对调)仍拼成一个正方形,并使正方形的每一行,每一列及两条对角线上的7个数之和都相等.请你开动脑筋,看看能不能想出以剪最少块数的方法达到以上要求.
有七张相同的纸条,恰好组成一个正方形,每张纸条上都依次写上1~7这七个数字,现在要把这些字条剪短后,左右对调(不能上下对调)仍拼成一个正方形,并使正方形的每一行,每一列及两条对角线上的7个数之和都相等.请你开动脑筋,看看能不能想出以剪最少块数的方法达到以上要求.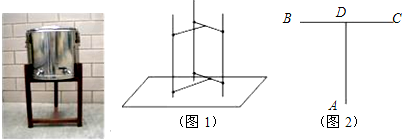
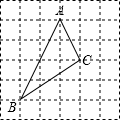 如图,三角形ABC在正方形网格中(图中每个小正方形的边长均为1个单位长度),若点A的坐标为(0,3),点B的坐标为(-2,-1),按要求解下列问题:
如图,三角形ABC在正方形网格中(图中每个小正方形的边长均为1个单位长度),若点A的坐标为(0,3),点B的坐标为(-2,-1),按要求解下列问题: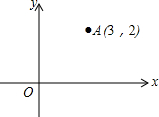 如图,在平面直角坐标系中,点A的坐标为(3,2),能否建立一个新的平面直角坐标系x′O′y′,使得在新的x′O′y′中,点O的坐标变为(-3,-2)?如果可以,请画出新的坐标系;若不可以,请说明理由.
如图,在平面直角坐标系中,点A的坐标为(3,2),能否建立一个新的平面直角坐标系x′O′y′,使得在新的x′O′y′中,点O的坐标变为(-3,-2)?如果可以,请画出新的坐标系;若不可以,请说明理由.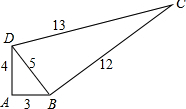 一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗?求出四边形ABCD的面积.
一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗?求出四边形ABCD的面积.