题目内容
2.如果|x-2y|+(x+y-3)2=0成立,那么xy=2.分析 利用非负数的性质列出方程组,求出方程组的解得到x与y的值,即可求出所求式子的值.
解答 解:∵|x-2y|+(x+y-3)2=0,
∴$\left\{\begin{array}{l}{x=2y}\\{x+y=3}\end{array}\right.$,
解得:x=2,y=1,
则原式=2,
故答案为:2.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
11. 如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
 如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )
如图,在?ABCD中,BC=10,sinB=$\frac{9}{10}$,AC=BC,则?ABCD的面积是( )| A. | 2$\sqrt{19}$ | B. | 6$\sqrt{19}$ | C. | 9$\sqrt{19}$ | D. | 18$\sqrt{19}$ |
7.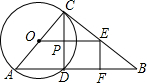 已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )
已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )
 已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )
已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )| A. | OE∥AB | B. | BC=2DE | C. | AC•DF=DE•CD | D. | DE=$\sqrt{2}$PD |
 如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.
如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.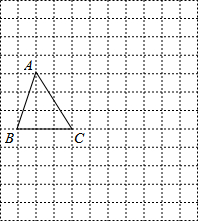 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格的交点). 如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).
如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).