题目内容
12.某施工工地安放了一个圆柱形饮水桶的木制支架某施工工地安放了一个圆柱形饮水桶的木制支架(如图1所示),若不计木条的厚度,其俯视图如图2所示.已知AD垂直平分BC,AD=BC=48cm,则圆柱形饮水桶的底面半径的最大值是30cm.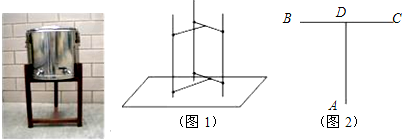
分析 当圆柱形饮水桶的底面半径最大时,圆外接于△ABC;连接外心与B点,可通过勾股定理即可求出圆的半径.
解答 解:连接OB,如图,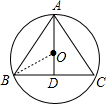
当⊙O为△ABC的外接圆时圆柱形饮水桶的底面半径的最大.
∵AD垂直平分BC,AD=BC=48cm,
∴O点在AD上,BD=24cm;
在Rt△0BD中,设半径为r,则OB=r,OD=48-r,
∴r2=(48-r)2+242,解得r=30.
即圆柱形饮水桶的底面半径的最大值为30cm.
故答案为:30
点评 此题主要考查了垂径定理的推论和勾股定理,具备把实物图转化为几何图形的能力是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.2014年舟山全市经济运行情况显示,舟山2014年实现第三产业增加值490.77亿元,其中490.77用科学记数法表示为( )
| A. | 4.9077×102 | B. | 49.077×102 | C. | 4.9077×103 | D. | 49.077×103 |
7.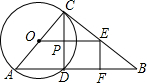 已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )
已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )
 已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )
已知,如图,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,EF⊥AB于F,连接OE交DC于点P,则下列结论不正确的是( )| A. | OE∥AB | B. | BC=2DE | C. | AC•DF=DE•CD | D. | DE=$\sqrt{2}$PD |
4.解方程组$\left\{\begin{array}{l}{x+y=10}\\{x-2y=5}\end{array}\right.$时,消去x,得到的方程是( )
| A. | -y=15 | B. | -y=5 | C. | 3y=15 | D. | 3y=5 |
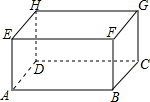 现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).
现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm). 已知:如图,∠1+∠2=180°,AD∥BC,DA平分∠BDF,
已知:如图,∠1+∠2=180°,AD∥BC,DA平分∠BDF,