题目内容
15．当a=6时，方程组$\left\{\begin{array}{l}ax+y=19\\ x-y=2\end{array}\right.$的解x与y的和是4．分析 根据方程组的解的概念，联立$\left\{\begin{array}{l}{x-y=2}\\{x+y=4}\end{array}\right.$求得x、y的值，代入ax+y=19解方程可得a的值．
解答 解：∵程组$\left\{\begin{array}{l}ax+y=19\\ x-y=2\end{array}\right.$的解x+y=4，
∴联立$\left\{\begin{array}{l}{x-y=2}\\{x+y=4}\end{array}\right.$，解得：$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$，
将x=3、y=1代入ax+y=19，得：3a+1=19，
解得：a=6．
故答案为：6．
点评 本题主要考查二元一次方程组的解的概念及解方程组的能力，根据方程组的解的概念得到新方程组是解题的关键．
练习册系列答案
相关题目
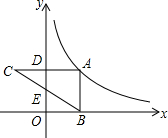如图，点A在反比例函数y=$\frac{k}{2x}$（x＞0）的图象上，过点A作AD⊥y轴于点D，延长AD至点C，使CD=AD，过点A作AB⊥x轴于点B，连结BC交y轴于点E．若△ABC的面积为6，则k的值为12．
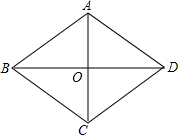已知：如图，菱形花坛ABCD周长是80m，∠ABC=60°，沿着菱形的对角线修建了两条小路AC和BD，相交于O点．
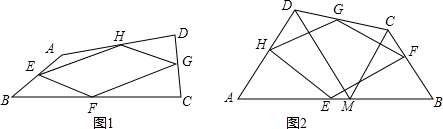
如图，将?ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．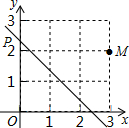
如图，点M的坐标为（3，2），动点P从点O出发，沿y轴以每秒1个单位的速度向上移动，且过点P的直线l：y=-x+b也随之移动，若点M关于l的对称点落在坐标轴上，设点P的移动时间为t，则t的值是2或3．