题目内容
7.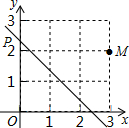 如图,点M的坐标为(3,2),动点P从点O出发,沿y轴以每秒1个单位的速度向上移动,且过点P的直线l:y=-x+b也随之移动,若点M关于l的对称点落在坐标轴上,设点P的移动时间为t,则t的值是2或3.
如图,点M的坐标为(3,2),动点P从点O出发,沿y轴以每秒1个单位的速度向上移动,且过点P的直线l:y=-x+b也随之移动,若点M关于l的对称点落在坐标轴上,设点P的移动时间为t,则t的值是2或3.
分析 找出点M关于直线l在坐标轴上的对称点E、F,如图所示.求出点E、F的坐标,然后分别求出ME、MF中点坐标,最后分别求出时间t的值.
解答 解:如图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F为点M在坐标轴上的对称点.
过点M作MD⊥x轴于点D,则OD=3,MD=2.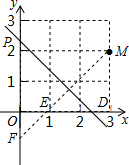
由直线l:y=-x+b可知∠PDO=∠OPD=45°,
∴∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,-1).
∵M(3,2),F(0,-1),
∴线段MF中点坐标为($\frac{3}{2}$,$\frac{1}{2}$).
直线y=-x+b过点($\frac{3}{2}$,$\frac{1}{2}$),则$\frac{1}{2}$=-$\frac{3}{2}$+b,解得:b=2,
∴t=2.
∵M(3,2),E(1,0),
∴线段ME中点坐标为(2,1).
直线y=-x+b过点(2,1),则1=-2+b,解得:b=3,
∴t=3.
故点M关于l的对称点,当t=2时,落在y轴上,当t=3时,落在x轴上.
故答案为2或3.
点评 考查了一次函数的图象与几何变换.注意在x轴、y轴上均有点M的对称点,不要漏解;其次注意点E、F坐标以及线段中点坐标的求法.

练习册系列答案
相关题目
2.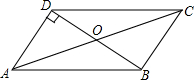 如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
 如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
12.下列说法正确的有( )
①△ABC在平移过程中,对应线段一定平行;
②△ABC在平移过程中,对应线段一定相等;
③△ABC在平移过程中,对应角一定相等;
④△ABC在平移过程中,图形大小不改变.
①△ABC在平移过程中,对应线段一定平行;
②△ABC在平移过程中,对应线段一定相等;
③△ABC在平移过程中,对应角一定相等;
④△ABC在平移过程中,图形大小不改变.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.一元二次方程x2-3x+1=0的两根为x1、x2,则x1+x2=( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
 如图,在平面直角坐标系中,矩形OABC的顶点A.C的坐标分别为(10,0),(0,3),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(1,3)或(4,3)或(9,3).
如图,在平面直角坐标系中,矩形OABC的顶点A.C的坐标分别为(10,0),(0,3),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(1,3)或(4,3)或(9,3).