题目内容
20. 如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.(1)求证:四边形ABEC是平行四边形;
(2)连接AC、BE,若四边形ABEC是矩形,则∠AFC与∠D应满足什么数量关系?并说明理由.
分析 (1)根据平行四边形的性质得到AB∥CD,AB=CD,然后根据CE=DC,得到AB=EC,AB∥EC,利用一组对边平行且相等的四边形是平行四边形判断即可;
(2)由(1)得的结论先证得四边形ABEC是平行四边形,通过角的关系得出FA=FE=FB=FC,AE=BC,得证.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵CE=DC,
∴AB=EC,AB∥EC,
∴四边形ABEC是平行四边形,
(2)当∠AFC=2∠D,四边形ABEC是矩形,
理由:∵AB=EC,AB∥EC,
∴四边形ABEC是平行四边形,
∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,
∴∠ABC=∠D,
又∵∠AFC=2∠D,
∴∠AFC=2∠ABC,
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
点评 此题考查了平行四边形的判定与性质和性质及矩形的判定,关键是先由平行四边形的性质证三角形全等,然后推出平行四边形通过角的关系证矩形.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
8.利用平方差公式计算20122-20132的结果是( )
| A. | 1 | B. | -1 | C. | 4025 | D. | -4025 |
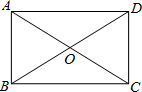 如图,矩形ABCD中,对角线AC和BD相交于点0,OD=AD,则sin∠OBA=$\frac{1}{2}$.
如图,矩形ABCD中,对角线AC和BD相交于点0,OD=AD,则sin∠OBA=$\frac{1}{2}$.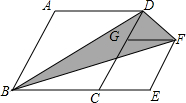 如图,菱形ABCD和菱形CEFG,AB=2,∠A=120°,点G在CD上,点B,C,E在同一条直线上,连接BD,BF,则△BDF的面积为$\sqrt{3}$.
如图,菱形ABCD和菱形CEFG,AB=2,∠A=120°,点G在CD上,点B,C,E在同一条直线上,连接BD,BF,则△BDF的面积为$\sqrt{3}$.