题目内容
4.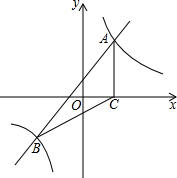 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点(1)求一次函数与反比例函数的解析式.
(2)根据条件,直接写出$\frac{m}{x}$>kx+b的解集.
(3)过点A作AC⊥x轴,垂足为C,求S△ABC.
分析 (1)首先把A的坐标代入反比例函数关系式中可以求出m,再把B(1,n)代入反比例函数关系式中可以求出n的值,然后利用待定系数法就可以求出一次函数的解析式;
(2)根据A、B的横坐标结合图象即可得出答案.
(3)利用三角形的面积公式即可直接求解.
解答  解:(1)∵点A(2,3)在反比例函数y=$\frac{m}{x}$的图象上,
解:(1)∵点A(2,3)在反比例函数y=$\frac{m}{x}$的图象上,
∴m=2×3=6.
∴反比例函数的表达式为y=$\frac{6}{x}$.
∵点B(-3,n)也在反比例函数y=$\frac{6}{x}$的图象上,
∴n=-2,即B(-3,-2).
把点A(2,3),点B(-3,-2)代入一次函数y=kx+b中,
得$\left\{\begin{array}{l}{2k+b=3}\\{-3k+b=-2}\end{array}\right.$解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$.
∴一次函数解析式为y=x+1.
(2)∵A(2,3),B(-3,-2),
观察图象可知,当x<-3或0<x<2时,一次函数的图象在反比例函数图象的下方,
∴不等式$\frac{m}{x}$>kx+b的解集是x<-3或0<x<2.
(3)作BD⊥AC于E.则AC=3,BE=5,
∴S△ABC=$\frac{1}{2}$AC•BE=$\frac{1}{2}$×3×5=$\frac{15}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题,用待定系数法求出反比例函数的解析式,函数的图象的应用以及三角形的面积公式,主要考查学生的计算能力和观察图象的能力,用了数形结合思想.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
14.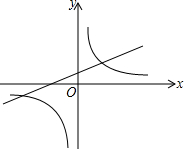 如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )
如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )
 如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )
如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )| A. | k<1 | B. | k>0 | C. | k<0 | D. | k>1 |
19.下列各组数中,不是勾股数的是( )
| A. | 13、5、12 | B. | 4、5、6 | C. | 3、4、5 | D. | 15、20、25 |
9.下列运算正确的是( )
| A. | 2x+3y=5 | B. | 4x2y-5xy2=-x2y | C. | a5+a6=a11 | D. | 3ab2-b2a=2ab2 |

 如图为了确定各建筑物的位置:
如图为了确定各建筑物的位置: 如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )
如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )