题目内容

19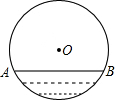．如图，水平放置一个油管其截面直径为100cm其中有油部分油面宽AB为80cm，截面上有油部分的油面高为20cm．

分析 本题是已知圆的直径和弦长，求油的最大深度其实就是弧AB的中点到弦AB的距离，可以转化为求弦心距的问题，利用垂径定理来解决．

解答 解：过点O作OM⊥AB交AB与M，交弧AB于点E；
连接OA，在Rt△OAM中：
OA=50cm，AM=$\frac{1}{2}$AB=40cm，
根据勾股定理可得OM=30cm，
则油的最大深度ME为20cm．
故答案为20．

点评 此题主要考查的是垂径定理及勾股定理的应用．解题的关键是正确的构造直角三角形．

练习册系列答案
相关题目
9．下列运算正确的是（　　）
A．2x+3y=5B．4x2y-5xy2=-x2yC．a5+a6=a11D．3ab2-b2a=2ab2
10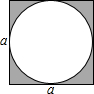．如图，阴影部分的面积是（　　）
A．（1-$\frac{π}{4}$）a2B．（1-$\frac{π}{2}$）a2C．（1-$\frac{π}{4}$a）aD．$\frac{3π}{4}$a2
7．把两个全等的直角三角形ABC和DEF重叠在一起，其中∠A=60°，AC=1．固定△ABC不动，将△DEF进行如下操作：

（1）如图1，将△DEF沿线段AB向右平移（即D点在线段AB内移动），连接DC，CF，FB，四边形CDBF的形状在不断的变化，但它的面积不变化，其面积为$\frac{\sqrt{3}}{2}$；
（2）如图2，将△DEF的D点固定在AB的中点，然后绕D点按顺时针方向旋转△DEF，使DF落在AB边上，此时F点恰好与B点重合，连接AE，则sinα的值等于$\frac{\sqrt{21}}{14}$．
14．如图，⊙O的直径AB=2，∠ABC=30°，C、D在圆上，则下列结论中：①∠CDB=60°；②弦AC=1；③∠ABD=30°；④OD=1，其中正确的是个数为（　　）
A．4个B．3个C．2个D．1个
4．己知抛物线y=2x2-12x+6
（1）用配方法确定它的顶点坐标、对称轴；
（2）x取何值时，y随x的增大而减小？
11．在关系式y=3x+4中，当自变量x=7时，因变量y的值是（　　）
A．1B．7C．25D．31
8．为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图．

（Ⅰ）小明一共调查了多少户家庭？
（Ⅱ）求所调查家庭5月份用水量的中位数、众数、平均数；
（Ⅲ）若该小区有400户居民，请你估计这个小区5月份的用水量．
9．若y=（m-1）x|m|-2是反比例函数，则m的值为（　　）
A．m=2B．m=-1C．m=1D．m=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网