题目内容
3. 如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
分析 由正方形的性质可知;AC平分∠DAB,然后由角平分线的性质可知GE=GF,从而可证明四边形EGFA为正方形,故此四边形AFGE与四边形ABCD相似.
解答 证明;∵∠GEA=∠EAF=∠GFA=90°,
∴四边形EAFG为矩形.
∵四边形ABCD为正方形,
∴AC平分∠DAB.
又∵GE⊥AD,GF⊥AB,
∴GE=GF.
∴四边形EAFG为正方形.
∴四边形AFGE与四边形ABCD相似.
点评 本题主要考查的是相似多边形的判定、正方形的判定、角平分线的性质,证得四边形EAFG为正方形是解题的关键.

练习册系列答案
相关题目
14. 如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )
如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )
 如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )
如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11.在关系式y=3x+4中,当自变量x=7时,因变量y的值是( )
| A. | 1 | B. | 7 | C. | 25 | D. | 31 |
15.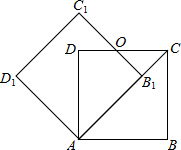 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{2}$ | D. | 1 |
 如图为了确定各建筑物的位置:
如图为了确定各建筑物的位置: