题目内容
9．设a，b是方程x2+2x-2019=0的两个不相等的实数根．（1）a+b=-2；ab=-2019；2a2+4a=4038；
（2）求代数式a2+3a+b的值．
分析 （1）直接利用根与系数的关系可得a+b；ab，利用方程的解的定义得出a2+2a=2019进而求出2a2+4a即可；
（2）a2+3a+b变形为a2+2a+a+b，利用（1）的a2+2a=2019可得结果．
解答 解：由根与系数的关系得：
a+b=-2，ab=-2019，
∵a是方程x2+2x-2019=0的实数根，
∴a2+2a=2019，
∴2a2+4a=2×2019=4038；
故答案为：-2，-2019，4038；
（2）a2+3a+b=a2+2a+a+b
=2019-2
=2017．
点评 此题主要考查了根与系数的关系以及方程的解，得出a，b的关系是解题关键．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
20．某公司需要从甲、乙两个仓库向A、B两地分别运送100t和50t的物资．已知该物资在甲仓库有80t，乙仓库有70t．从甲、乙两个仓库运送物资到A、B两地的运费如下表：
（1）设从甲仓库运送到A地的物资为xt，求运送的总运费y（单位：元）与x（单位：t）之间的函数解析式，并写出x的取值范围．
（2）请你设计出运费最低的运送方案，并求出最低运费．
| 目的地 | 运费/（元/t） | |
| 甲仓库 | 乙仓库 | |
| A地 | 140 | 200 |
| B地 | 100 | 80 |
（2）请你设计出运费最低的运送方案，并求出最低运费．
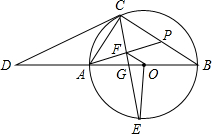如图，AB为⊙O的直径，CD切⊙O于点C，与BA的延长线交于点D，OE⊥AB交⊙O于点E，连接CA、CE、CB，CE交AB于点G，过点A作AF⊥CE于点F，延长AF交BC于点P．
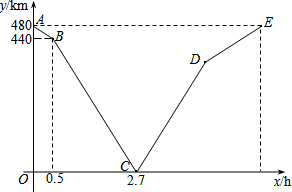一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设一辆车先出发xh后，另一辆车也开始行驶，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系．根据图象解决以下问题：
1．若a+b=3，则代数式（$\frac{{b}^{2}}{a}$-a）÷$\frac{a-b}{a}$的值为（ ）
| A． | 3 | B． | -3 | C． | $\frac{1}{3}$ | D． | -$\frac{1}{3}$ |
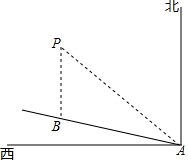如图，一艘船以每小时24海里的速度向北偏西75°方向航行，在点A处测得灯塔P在船的西北方向，航行40分钟后到达点B处，这时灯塔P恰好在船的正北方向，已知距离灯塔9海里以外的海区为安全航行区域，问这艘船能否按原方向继续向前航行？为什么？
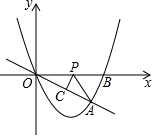如图，在平面直角坐标系中，直线OA与抛物线y=ax2+bx交于原点O和点A（4，-2），点B（5，0）在抛物线上，点P是x轴上一动点，PC⊥OA于点C，连接PA．