题目内容
17.解方程组:$\left\{\begin{array}{l}{{x}^{2}+4xy+4y=1}\\{{x}^{2}+xy=0}\end{array}\right.$.分析 把②通过因式分解化为两个二元一次方程,把这两个二元一次方程分别与①组成方程组,求解即可.
解答 解:$\left\{\begin{array}{l}{{x}^{2}+4xy+4y=1①}\\{{x}^{2}+xy=0②}\end{array}\right.$
由②得,x+y=0,x=0,
把这两个方程与①组成方程组得
$\left\{\begin{array}{l}{{x}^{2}+4xy+4y=1}\\{x+y=0}\end{array}\right.\left\{\begin{array}{l}{{x}^{2}+4xy+4y=1}\\{x=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=0}\\{y=\frac{1}{4}}\end{array}\right.\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.\left\{\begin{array}{l}{x=-\frac{1}{3}}\\{y=\frac{1}{3}}\end{array}\right.$
所以方程组的解为:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=\frac{1}{4}}\end{array}\right.\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=1}\end{array}\right.\left\{\begin{array}{l}{{x}_{3}=-\frac{1}{3}}\\{{y}_{3}=\frac{1}{3}}\end{array}\right.$
点评 本题考查的是二元二次方程组的解法,解答时,用代入法比较简单,如果其中的二元二次方程可以因式分解化为两个二元一次方程,与另一个方程组成两个二元一次方程组,解答更简单.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 一个游戏中奖的概率是$\frac{1}{10}$,则做10次这样的游戏一定会中奖 | |
| B. | 为了了解一批炮弹的杀伤半径,应采用全面调查的方式 | |
| C. | 一组数据8,7,7,10,6,7,9的众数和中位数都是7 | |
| D. | 若甲组数据的方差是0.1,乙组数据的方差是0.2,则乙组数据比甲组数据波动小 |
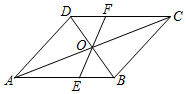 如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.