Question

4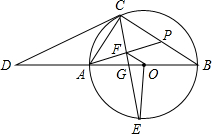．如图，AB为⊙O的直径，CD切⊙O于点C，与BA的延长线交于点D，OE⊥AB交⊙O于点E，连接CA、CE、CB，CE交AB于点G，过点A作AF⊥CE于点F，延长AF交BC于点P．
（Ⅰ）求∠CPA的度数；
（Ⅱ）连接OF，若AC=$\sqrt{3}$，∠D=30°，求线段OF的长．

Answer 1

分析 （Ⅰ）连接AE，由OA=OB且OE⊥AB知∠OEG+∠AEC=45°，再证∠OEG=∠BAP、∠AEC=∠ABP，在△ABP中利用三角形外角性质可得答案；
（Ⅱ）由切线性质及∠D=30°可得∠AOC=∠OAC=60°，在Rt△ABC中求得BC=3，由∠APC=45°、∠ACP=90°得CP=AC=$\sqrt{3}$，可知BP=3-$\sqrt{3}$，证OF为△ABP中位线可得答案．

解答 解：（Ⅰ）如图，连接AE，

∵OE⊥AB，OA=OE，
∴∠AOE=90°，∠AEO=45°，
∴∠OEG+∠OGE=90°，
∵AF⊥CE，
∴∠AFG=90°，
∴∠FAG+∠AGF=90°，
∵∠AGF=∠OGE，
∴∠OEG=∠BAP，
∵∠AEC=∠ABC，
∴∠APC=∠ABC+∠BAP=∠AEC+∠OEG=∠AEO=45°；

（Ⅱ）连接OC，
∵CD是⊙O的切线，
∴∠DCO=90°，
∵∠D=30°，
∴∠AOC=60°，
∵OA=OC，
∴∠BAC=60°，
在Rt△ABC中，AC=$\sqrt{3}$，
∴BC=ACtan∠BAC=$\sqrt{3}$×$\sqrt{3}$=3，
由（1）知，AC=CP=$\sqrt{3}$，
∴BP=BC-CP=3-$\sqrt{3}$，
∵AF⊥CE，
∴AF=PF，
∵OA=OB，
∴OF=$\frac{1}{2}$BP=$\frac{3-\sqrt{3}}{2}$．

点评 本题主要考查切线的性质、圆周角定理及解直角三角形等知识点，熟练掌握圆的切线的性质及圆周角定理、三角形外角的性质等是解题的关键．