题目内容
20. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C2015.
若P(m,2),在第2015段抛物线C2015上,则m=6043或6044.
分析 根据图象的旋转变化规律以及二次函数的平移规律得出平移后解析式,进而求出m的值.
解答 解:∵y=-x(x-3)(0≤x≤3),
∴图象与x轴交点坐标为:(0,0),(3,0),
∴OA1=3,
∵将C1绕点A1旋转180°得C2,交x轴于点A2;
∴OA2=2×3=6,
同理可得OA3=3×3=9,
…
∴OA2015=2014×3=6042,
∴第2015段抛物线C2015可看作第1段抛物线y=-x2+3x(0≤x≤3)向右平移6042个单位,
当y=2时,-x2+3x=2,解得x1=1,x2=2,
∴点(1,2)和点(2,2)向右平移6042个单位所得对应点的坐标为(6043,2),(6044,2),
∴m的值为6043或6044.
故答案为:6043或6044.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.也考查了从特殊到一般解决规律型问题的方法.

练习册系列答案
相关题目
13.二次函数y=(x-1)2+2的最小值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
5.下列各组数中,是勾股数的为( )
| A. | 1,1,2 | B. | 7,24,25 | C. | 1.5,2,2.5 | D. | 6,12,13 |
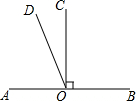 如图,已知直线AB,线段CO⊥AB于O,∠AOD=$\frac{1}{2}$∠BOD,求∠COD的度数.
如图,已知直线AB,线段CO⊥AB于O,∠AOD=$\frac{1}{2}$∠BOD,求∠COD的度数. 已知抛物线的顶点为(0,4)且与x轴交于(-2,0),(2,0).
已知抛物线的顶点为(0,4)且与x轴交于(-2,0),(2,0).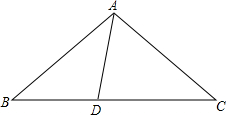 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,∠ADB=100°,则∠BAC的度数为100°.
如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,∠ADB=100°,则∠BAC的度数为100°.