题目内容
4. 如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为(50-$\frac{50\sqrt{3}}{3}$)m.
如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为(50-$\frac{50\sqrt{3}}{3}$)m.
分析 如图,过点A作AM⊥DC于点M,过点B作BN⊥DC于点N.则AM=BN.通过解直角△ACM和△BCN分别求得CM、CN的长度,则易得MN=AB.
解答  解:如图,过点A作AM⊥DC于点M,过点B作BN⊥DC于点N.
解:如图,过点A作AM⊥DC于点M,过点B作BN⊥DC于点N.
则AB=MN,AM=BN.
在直角△ACM,∵∠ACM=45°,AM=50m,
∴CM=AM=50m.
∵在直角△BCN中,∠BCN=∠ACB+∠ACD=60°,BN=50m,
∴CN=$\frac{BN}{tan60°}$=$\frac{50}{\sqrt{3}}$=$\frac{50\sqrt{3}}{3}$(m),
∴MN=CM-CN=50-$\frac{50\sqrt{3}}{3}$(m).
则AB=MN=(50-$\frac{50\sqrt{3}}{3}$)m.
故答案是:(50-$\frac{50\sqrt{3}}{3}$).
点评 本题考查了解直角三角形的应用.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.

练习册系列答案
相关题目
5.-$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
19.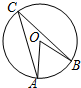 如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )
如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )
 如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )
如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )| A. | 60° | B. | 50° | C. | 45° | D. | 30° |
14.下列各图中,∠1与∠2互为余角的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,正方形网格中的每一个小正方形的边长为1个单位长度,题中所给各点均在格点上.
如图,正方形网格中的每一个小正方形的边长为1个单位长度,题中所给各点均在格点上.