题目内容
16.若等腰三角形的底边长是10cm,其面积是25$\sqrt{3}$cm2,则底角的正弦值等于$\frac{\sqrt{3}}{2}$.分析 根据题意可以求得等腰三角形底边上的高,从而可以求得等腰三角形的腰长,进而可以求得底角的正弦值.
解答 解:设等腰三角形底边上的高为xcm,
∵等腰三角形的底边长是10cm,其面积是25$\sqrt{3}$cm2,
∴$\frac{10x}{2}=25\sqrt{3}$,
解得,x=$5\sqrt{3}$,
∴等腰三角形的腰长为:$\sqrt{(5\sqrt{3})^{2}+{5}^{2}}=10$cm,
∴底角的正弦值为:$\frac{5\sqrt{3}}{10}=\frac{\sqrt{3}}{2}$,
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查解直角三角形、等腰三角形的性质、勾股定理,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
7.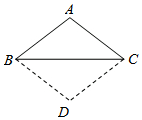 如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )
如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )
 如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )
如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )| A. | 一组邻边相等的平行四边形是菱形 | |
| B. | 四条边相等的四边形是菱形 | |
| C. | 对角线互相垂直的平行四边形是菱形 | |
| D. | 对角线互相垂直的平分四边形是菱形 |
8.已知多项式(a-3)x3+x|b|-2x+b+2是关于x的二次三项式,则a、b的值分别为( )
| A. | a=3,b=2 | B. | a=0,b=0 | C. | a=3,b=-2 | D. | a=-3,b=2 |
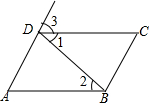 推理填空:
推理填空: 如图,已知∠BAC=∠ABD,
如图,已知∠BAC=∠ABD,