题目内容
11. 推理填空:
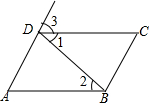
推理填空:如图:若∠1=∠2
则AB∥CD(推理:内错角相等,两直线平行)
若∠DAB+∠ABC=180°
则AD∥CB(推理:同旁内角互补,两直线平行)
分析 根据平行线的判定定理进行解答即可.
解答 解:∵∠1=∠2,
∴AB∥CD;
∵∠DAB+∠ABC=180°,
∴AD∥BC.
故答案为:AB∥CD,内错角相等,两直线平行;AD∥CB,同旁内角互补,两直线平行.
点评 本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
相关题目
6.毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究:
现通过观察思考后,已知第六层的“正方形数”几何点数是11,第n层的“三角形数”几何点数是n,则:第六层的“三角形数”的几何点数是______;第n层的“正方形数”几何点数是______.以下选项正确的是( )
| 名称及图形 几何点数 层数 | 三角形数 | 正方形数 |
 |  | |
| 第一层几何点数 | 1 | 1 |
| 第二层几何点数 | 2 | 3 |
| 第三层几何点数 | 3 | 5 |
| … | … | … |
| 第六层几何点数 |  |  |
| … | … | … |
| 第n层几何点数 |  |  |
| A. | 6、2n-1 | B. | 6、2n+1 | C. | 6、n+2 | D. | n、2n-1 |
 已知实数a,在数轴上如图所示,则|a-1|=1-a.
已知实数a,在数轴上如图所示,则|a-1|=1-a. 如图,∠BDC=2∠ACB,CE=BD,EF∥AB,求证:AB=FB.
如图,∠BDC=2∠ACB,CE=BD,EF∥AB,求证:AB=FB. 如图所示,在△ABC中,AB=AC,BD=DC,DE∥AB交AC于点E,BF⊥AC于F,交AD于P,PM⊥AB于M,下面五个结论中,正确的有①②⑤.(只填序号)
如图所示,在△ABC中,AB=AC,BD=DC,DE∥AB交AC于点E,BF⊥AC于F,交AD于P,PM⊥AB于M,下面五个结论中,正确的有①②⑤.(只填序号)