题目内容
18. 如图,等边△ABC的边长为1,在边AB上有一点P,Q为BC延长线上的一点,且CQ=PA,过点P作PE⊥AC于点E,连接PQ交AC于点D,则DE的长为$\frac{1}{2}$.
如图,等边△ABC的边长为1,在边AB上有一点P,Q为BC延长线上的一点,且CQ=PA,过点P作PE⊥AC于点E,连接PQ交AC于点D,则DE的长为$\frac{1}{2}$.
分析 过P作BC的平行线至AC于F,通过求证△PFD和△QCD全等,推出FD=CD,再通过证明△APF是等边三角形和PE⊥AC,推出AE=EF,即可推出AE+DC=EF+FD,可得ED=$\frac{1}{2}$AC,即可推出ED的长度.
解答 解:过P做BC的平行线至AC于F,
∴∠Q=∠FPD,
∵等边△ABC,
∴∠APF=∠B=60°,∠AFP=∠ACB=60°,
∴△APF是等边三角形,∴AP=PF,AP=CQ,
∵AP=CQ,
∴PF=CQ,
∵在△PFD和△QCD中,
$\left\{\begin{array}{l}{∠FPD=∠Q}\\{∠PDF=∠QDC}\\{PF=CQ}\end{array}\right.$,
∴△PFD≌△QCD(AAS),
∴FD=CD,∵PE⊥AC于E,△APF是等边三角形,∴AE=EF,
∴AE+DC=EF+FD,
∴ED=$\frac{1}{2}$AC,
∵AC=1,
∴DE=$\frac{1}{2}$.
故答案为$\frac{1}{2}$.
点评 本题主要考查等边三角形的判定与性质、平行线的性质、全等三角形的判定与性质,关键在于正确地作出辅助线,熟练运用相关的性质、定理,认真地进行计算.

练习册系列答案
相关题目
10.在平行四边形、矩形、菱形、正方形中,既是轴对称图形又是中心对称图形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.若a>b,则下列式子中一定成立的是( )
| A. | a-2<b-2 | B. | $\frac{a}{2}$>$\frac{b}{2}$ | C. | 2a>b | D. | 3-a>3-b |
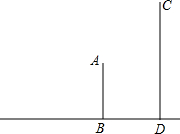 已知如图,从20米高的甲楼A望乙楼顶C处的仰角是30°,望乙楼底D处的俯角是45°,求乙楼的高度(精确到0.1米,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
已知如图,从20米高的甲楼A望乙楼顶C处的仰角是30°,望乙楼底D处的俯角是45°,求乙楼的高度(精确到0.1米,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732). 已知:如图所示,E为正方形ABCD外一点,AE=AD,∠ADE=75°,求∠AEB的度数.
已知:如图所示,E为正方形ABCD外一点,AE=AD,∠ADE=75°,求∠AEB的度数.