题目内容
13．根据不等式的基本性质，可将“mx＜2”化为“x$＞\frac{2}{m}$”，则m的取值范围是m＜0．分析 利用不等式的基本性质求出m的范围即可．
解答 解：∵根据不等式的基本性质，可将“mx＜2”化为“x$＞\frac{2}{m}$”，
∴m＜0，
故答案为：m＜0
点评 此题考查了不等式的性质，熟练掌握不等式的基本性质是解本题的关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，过E点作EF∥DC交BC的延长线于点F，连接CD．
1．下列关于x的方程：①ax2+bx+c=0；②3（x-9）2-（x+1）2=1；③x+3=$\frac{1}{x}$；④x2=0；⑤$\sqrt{x+1}=x-1$．其中是一元二次方程有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
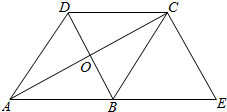如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连结CE，若∠E=50°，求∠BAO的大小．
如图，等边△ABC的边长为1，在边AB上有一点P，Q为BC延长线上的一点，且CQ=PA，过点P作PE⊥AC于点E，连接PQ交AC于点D，则DE的长为$\frac{1}{2}$．
5．若点P（m-1，3）在第二象限，则m的取值范围是（ ）
| A． | m＞1 | B． | m＜1 | C． | m≥-1 | D． | m≤1 |
如图，已知△ABC的顶点坐标分别为A（-1，-1），B（-3，-3），C（0，-4），将△ABC先向右平移2个单位，再向上平移4个单位得△A′B′C′．