题目内容
11.某校准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.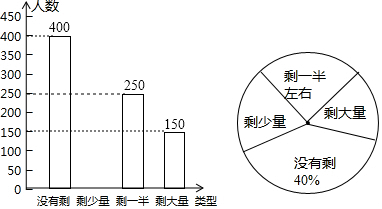
请根据统计图给出的信息,回答下列问题:
(1)这次被调查的同学共有1000名;
(2)求出“剩少量”饭菜的学生人数,并把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
分析 (1)根据“没有剩”的人数除以“没有剩”的人数所占的百分比,可得调查的人数;
(2)根据有理数的减法,可得“剩少量”的人数,根据“剩少量”的人数,可得答案;
(3)根据总人数乘以“食用一餐的人数与调查的人数比”,可得答案.
解答 解:(1)这次被调查的同学共有400÷40%=1000人.
(2)“剩少量”的人数1000-400-250-150=200人,
补充完整为: ;
;
(3)18000×$\frac{200}{1000}$=3600(人).
故学生一餐浪费的食物可供3600人食用一餐.
故答案为:1000.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
16.下列分式运算,正确的是( )
| A. | ${(\frac{2b}{3a})^2}=\frac{{2{b^2}}}{{3{a^2}}}$ | B. | $\frac{{{x^2}-4}}{x-2}=x-2$ | C. | $2x•\frac{1}{2x}=\frac{1}{{4{x^2}}}$ | D. | $\frac{1}{x-y}+\frac{1}{y-x}=0$ |
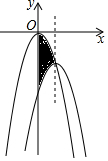 如图,在平面直角坐标系中,二次函数y=-3x2的图象经过平移得到二次函数y=-3x2+6x-6的图象,则二次函数y=-3x2图象的对称轴与两段抛物线所围成的阴影部分的面积为3.
如图,在平面直角坐标系中,二次函数y=-3x2的图象经过平移得到二次函数y=-3x2+6x-6的图象,则二次函数y=-3x2图象的对称轴与两段抛物线所围成的阴影部分的面积为3. 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图. 小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线:
小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线: