题目内容
19.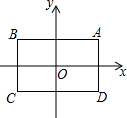 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
分析 根据位似变换的性质和中心对称图形的概念求出C′点的坐标,根据题意得到反比例函数n=$\frac{3}{m}$的图象经过C′点,代入计算即可.
解答 解:∵矩形A′B′C′D′与矩形ABCD是位似图形,A′B′=2AB,顶点A的坐标为(1,t),
∵矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,
∴点C的坐标为(-1,-t),矩形A′B′C′D′也关于点O成中心对称,
∴C′点的坐标是(-2,-2t),
∵mn=3,
即n=$\frac{3}{m}$,
∵以m,n为坐标(记为(m,n)的所有的点中,有且只有一个点落在矩形A′B′C′D′的边上,
∴反比例函数n=$\frac{3}{m}$的图象只经过点A′或C′,
∵矩形A′B′C′D′关于点O成中心对称,反比例函数n=$\frac{3}{m}$的图象关于点O成中心对称,
∴反比例函数n=$\frac{3}{m}$的图象经过C′点,
∴-2•(-2t)=3,
解得t=$\frac{3}{4}$.
故选:A.
点评 本题主要考查了位似变换问题,解答此题的关键是要明确:①两个图形必须是相似形;②对应点的连线都经过同一点;③对应边平行.

练习册系列答案
相关题目
14. 实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
 实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )| A. | -2a+b | B. | -b | C. | -2a-b | D. | b |
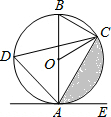 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠CAE=∠ADC.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠CAE=∠ADC.