题目内容
3. 如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
分析 (1)根据邻补角的定义确定出∠AOC和∠BOD,再根据角平分线的定义可得∠AOF=∠EOF,根据垂直的定义可得∠COF=∠DOF=90°,然后根据等角的余角相等求出∠DOE=∠ACO,从而最后得解;
(2)根据角平分线的定义求出∠AOF,再根据余角的定义求出∠AOC,然后根据对顶角相等解答.
解答 解:(1)∵直线AB,CD相交于点O,
∴∠AOC和∠BOD与∠AOD互补,
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∵OF⊥CD,
∴∠COF=∠DOF=90°,
∴∠DOE=∠ACO,
∴∠DOE也是∠AOD的补角,
∴与∠AOD互补的角有∠AOC,∠BOD,∠DOE;
(2)∵OF平分∠AOE,
∴∠AOF=$\frac{1}{2}$∠AOE=60°,
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF-∠AOF=90°-60°=30°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=30°.
点评 本题考查了余角和补角,对顶角相等的性质,角平分线的定义,难点在于(1)根据等角的余角相等确定出与∠AOD互补的第三个角.

练习册系列答案
相关题目
14. 实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
 实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )| A. | -2a+b | B. | -b | C. | -2a-b | D. | b |
18.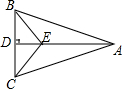 如图,AD⊥BC,垂足为D,BD=DC,则图中全等的三角形共有( )
如图,AD⊥BC,垂足为D,BD=DC,则图中全等的三角形共有( )
 如图,AD⊥BC,垂足为D,BD=DC,则图中全等的三角形共有( )
如图,AD⊥BC,垂足为D,BD=DC,则图中全等的三角形共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
8.下列图案中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
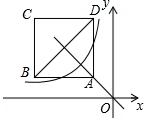 如图,正方形ABCD位于第二象限,边长为2,点A在直线y=-x上,点A的横坐标为-1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为-9≤k≤-1.
如图,正方形ABCD位于第二象限,边长为2,点A在直线y=-x上,点A的横坐标为-1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为-9≤k≤-1.