题目内容
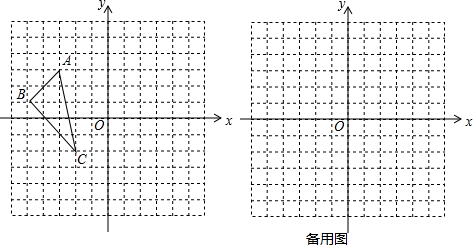
12.在△ABC中,若AC=15,BC=13,AB边上的高CD=12,则△ABC的周长为32或42.分析 作出图形,利用勾股定理列式求出AD、BD,再分CD在△ABC内部和外部两种情况求出AB,然后根据三角形的周长的定义解答即可.
解答 解:∵AC=15,BC=13,AB边上的高CD=12,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=9,
BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=5,
如图1,CD在△ABC内部时,AB=AD+BD=9+5=14,
此时,△ABC的周长=14+13+15=42,
如图2,CD在△ABC外部时,AB=AD-BD=9-5=4,
此时,△ABC的周长=4+13+15=32,
综上所述,△ABC的周长为32或42.
故答案为:32或42.
点评 本题考查了勾股定理的运用,难点在于分情况讨论求出AB的长,作出图形更形象直观.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
2.一个长方体的体积为x2-2xy+x,高是x,则这个长方体的底面积是( )
| A. | x-2y | B. | x+2y | C. | x-2y-1 | D. | x-2y+1 |
20.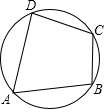 如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠C=1:2:4,则∠D为( )
如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠C=1:2:4,则∠D为( )
 如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠C=1:2:4,则∠D为( )
如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠C=1:2:4,则∠D为( )| A. | 90° | B. | 100° | C. | 108° | D. | 144° |
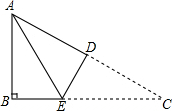 如图所示,在△ABC中,∠B=90°,将△ABC折叠,使点C与点A重合,折痕为DE,若△ABE的周长为7,AB比BC小1,则AB的长为8.
如图所示,在△ABC中,∠B=90°,将△ABC折叠,使点C与点A重合,折痕为DE,若△ABE的周长为7,AB比BC小1,则AB的长为8.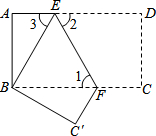 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.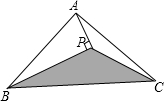 如图所示,三角形ABC的面积为1cm2.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是$\frac{1}{2}$cm2.
如图所示,三角形ABC的面积为1cm2.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是$\frac{1}{2}$cm2.