题目内容
已知:如图,OB、OC分别为定角∠AOD内部的两条动射线
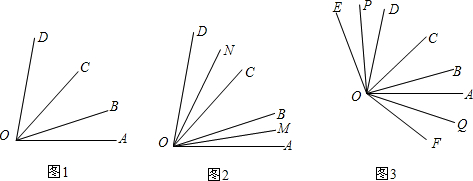
(1)当OB、OC运动到如图1的位置时,∠AOC+∠BOD=100°,∠AOB+∠COD=40°,求∠AOD的度数;
(2)在(1)的条件下(图2),射线OM、ON分别为∠AOB、∠COD的平分线,当∠COB绕着点O旋转时,下列结论:①∠AOM-∠DON的值不变;②∠MON的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.
(3)在(1)的条件下(图3),OE、OF是∠AOD外部的两条射线,∠EOB=∠COF=90°,OP平分∠EOD,OQ平分∠AOF,当∠BOC绕着点A旋转时,∠POQ的大小是否会发生变化?若不变,求出其度数;若变化,说明理由.
(1)当OB、OC运动到如图1的位置时,∠AOC+∠BOD=100°,∠AOB+∠COD=40°,求∠AOD的度数;
(2)在(1)的条件下(图2),射线OM、ON分别为∠AOB、∠COD的平分线,当∠COB绕着点O旋转时,下列结论:①∠AOM-∠DON的值不变;②∠MON的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.
(3)在(1)的条件下(图3),OE、OF是∠AOD外部的两条射线,∠EOB=∠COF=90°,OP平分∠EOD,OQ平分∠AOF,当∠BOC绕着点A旋转时,∠POQ的大小是否会发生变化?若不变,求出其度数;若变化,说明理由.

考点:角的计算,角平分线的定义
专题:
分析:(1)根据角的定义可知∠AOC+∠BOD=∠AOB+∠COD+2∠BOC,根据题意得出2∠BOC+40°=100°,求出∠BOC的度数,即可求出∠AOD的度数;
(2)根据角平分线的定义得出∠MON=∠CON+∠BOM+∠BOC=20°+30°=50°;
(3)先求得∠DOE+∠AOQ的值,再根据角平分线的定义得出∠POD+∠AOQ,再加上∠AOD即可得∠POQ的值.
(2)根据角平分线的定义得出∠MON=∠CON+∠BOM+∠BOC=20°+30°=50°;
(3)先求得∠DOE+∠AOQ的值,再根据角平分线的定义得出∠POD+∠AOQ,再加上∠AOD即可得∠POQ的值.
解答:解:(1)∵∠AOC+∠BOD=∠AOB+∠COD+2∠BOC,
∠AOC+∠BOD=110°,∠AOB+∠COD=50°,
∴110°=2∠BOC+50°,
∴∠BOC=30°,
∴∠AOD=∠BOC+∠AOB+∠COD=70°.
答:∠AOD为70°;
(2)②正确,∠MON=50°,
∵OM、ON分别为∠AOB、∠COD的平分线,
∴∠CON+∠BOM=
(∠AOB+∠COD)=
×40°=20°
∴∠MON=∠CON+∠BOM+∠BOC=20°+30°=50°.
故②正确,∠MON的度数为50°;
(3)∠POQ的大小不变为110°,
∵∠DOE+∠AOF=∠EOB+∠COF-∠BOC-∠AOD=90°+90°-30°-70°=80°.
∵OP平分∠EOD,OQ平分∠AOF,
∴∠POD+∠AOQ=
(∠DOE+∠AOF)=40°
∴∠POQ=∠POD+∠AOQ+∠AOD=40°+70°=110°
故∠POQ的大小不变为110°.
∠AOC+∠BOD=110°,∠AOB+∠COD=50°,
∴110°=2∠BOC+50°,
∴∠BOC=30°,
∴∠AOD=∠BOC+∠AOB+∠COD=70°.
答:∠AOD为70°;
(2)②正确,∠MON=50°,
∵OM、ON分别为∠AOB、∠COD的平分线,
∴∠CON+∠BOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠CON+∠BOM+∠BOC=20°+30°=50°.
故②正确,∠MON的度数为50°;
(3)∠POQ的大小不变为110°,
∵∠DOE+∠AOF=∠EOB+∠COF-∠BOC-∠AOD=90°+90°-30°-70°=80°.
∵OP平分∠EOD,OQ平分∠AOF,
∴∠POD+∠AOQ=
| 1 |
| 2 |
∴∠POQ=∠POD+∠AOQ+∠AOD=40°+70°=110°
故∠POQ的大小不变为110°.
点评:本题主要考查了角的有关计算以及角平分线的定义.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下列计算正确的是( )
| A、-2-(-2)=-4 |
| B、(-2)+(-2)=-4 |
| C、0×(-2013)=-2013 |
| D、(-6)÷(-2)=-3 |
 已知:如图,在△ABC中,AD是角平分线,BE⊥AD,交AD的延长线于点E,点F在AB上,且∠FBE=∠FEB,试说明:EF∥AC.
已知:如图,在△ABC中,AD是角平分线,BE⊥AD,交AD的延长线于点E,点F在AB上,且∠FBE=∠FEB,试说明:EF∥AC.