Question

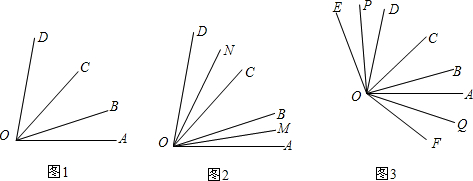
定义：如图1，射线OP与原点为圆心，半径为1的圆交于点P，记∠xOP=α，则点P的横坐标叫做角α的余弦值，记作cosα；点P的纵坐标叫做角α的正弦值，记作sinα；纵坐标与横坐标的比值叫做角α的正切值，记作tanα．
如：当α=45°时，点P的横坐标为cos45°=

2

2

，纵坐标为sin45°=

2

2

，即P（

2

2

，

2

2

）．又如：在图2中，∠xOQ=90°-α（α为锐角），PN⊥y轴，QM⊥x轴，易证△OQM≌△OPN，则Q点的纵坐标sin（90°-α）等于点P的横坐标cosα，得sin（90°-α）=cosα．

解决以下四个问题：
（1）当α=60°时，求点P的坐标；
（2）当α是锐角时，则cosα+sinα

 

1（用＞或＜填空），（sinα）²+（cosα）²=

 

；
（3）求证：sin（90°+α）=cosα（α为锐角）；
（4）求证：tan

α

2

=

1-cosα

sinα

（α为锐角）．

Answer 1

考点：圆的综合题

专题：

分析：（1）点P的横坐标为cos60°，纵坐标为sin60°，从而可得点P的坐标；
（2）结合图形可在△POM中，表示出cosα+sinα，继而与半径长1，比较即可；根据勾股定理可得（sinα）²+（cosα）²=1；
（3）画出图形，根据cosα及sin（90°+α）表示的实际意义，可得出结论；
（4）构造图形，如图，分别表示出tan

α

2

，及

1-cosα

sinα

表示的线段比，继而可得出结论．

解答：解：（1）点P的坐标为（cos60°，sin60°）=（

1

2

，

3

2

）．

（2）如图1所示：∠MOP=α，

∵半径为1，
∴cosα=

OM

OP

=OM，sinα=

PM

OP

=PM，
∴cosα+sinα=OM+PM＞OP=1；
∴（sinα）²+（cosα）²=PM²+OM²=OP²=1．

（3）如图2所示：∠MOP=α，

点P的纵坐标为sin（90°+α），值为OM的长度，cosα=

OM

OP

=OM，
∴sin（90°+α）=cosα．
（4）如图3所示：∠AOQ=∠POQ=

α

2

，∠AOP=α，
则cosα=

OM

OP

=OM，sinα=

PM

OP

=PM，
∴

1-cosα

sinα

=

AM

PM

=tan∠APM，
∵OQ是∠AOP的角平分线，
∴OQ⊥AP，
∴∠AOQ+∠OAP=90°，
∵∠APM+∠OAP=90°，
∴∠AOP=∠APM，
即

α

2

=∠APM，
∴tan

α

2

=tan∠APM=

1-cosα

sinα

．

点评：本题考查了圆的综合及锐角三角函数的定义，解答本题的关键是仔细审题，理解题意，将所求解问题转化为我们学过的知识求解．