题目内容
4.某水果店出售一种水果,每只定价20元时,每周可卖出300只.试销发现:(1)每只水果每降价1元,每周可多卖出25只.设现在定价每只x元(x<20),一周销售收入为y元,则y与x的函数关系式为W=-25x2+800x;
(2)每只水果每涨价1元,每周将少卖出10只,如何定价,才能使一周销售收入最多?
(3)根据以上信息,你认为应当如何定价才能使一周销售收入最多?
分析 (1)设销售收入为W元,售价为x元,根据销售收入=售价×数量就可以表示出W与x之间案的关系式;
(2)设销售收入为M元,售价为a元,根据销售收入=售价×数量就可以表示出M与a之间案的关系式,由函数的性质就可以得出结论;
(3)根据(1)、(2)的结论进行比较就可以求出结论.
解答 解:(1)设销售收入为W元,售价为x元,由题意,得
W=x[(20-x)×25+300],
W=-25x2+800x,
(2)设销售收入为M元,售价为a元,由题意,得
M=a[300-(a-20)×10],
M=-10(a-25)2+6250
∴a=-10<0,
∴a=25时,M最大=6250,
∴定价为25元时,一周销售收入最多为6250元;
(3)∴W=-25(x-16)2+6400.
∴a=-25<0,
∴x=16时,W最大=6400.
∴定价为16元时,一周销售收入最多为6400元;
∵6400>6250,
∴当定价为16元时,才能使一周销售收入最多.
点评 本题考查了销售问题的数量关系销售收入=售价×数量的运用,二次函数的解析式的性质的运用,解答时求出二次函数的解析式是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.已知关于x的方程5(x-a)=-2a的根大于关于x的方程3(x-a)=2(x+a)的根,则a应是( )
| A. | 不为0的数 | B. | 正数 | C. | 负数 | D. | 大于-1的数 |
12.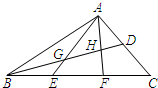 如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
 如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{7}{10}$ | C. | $\frac{6}{11}$ | D. | $\frac{11}{20}$ |
19.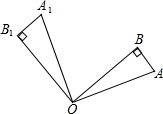 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )| A. | 125° | B. | 65° | C. | 75° | D. | 50° |
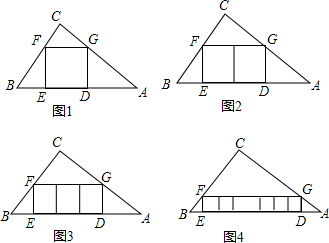
 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.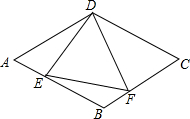 如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.
如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.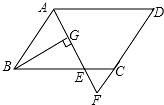 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求:
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求: