题目内容
16. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.
分析 (1)根据等边三角形性质求出∠B=∠C=60°,根据等式性质求出∠BAD=∠CDE,即可证明△ABD∽△DCE;
(2)由(1)知道△ABD∽△DCE,对应边成比例得出$\frac{AB}{DC}=\frac{BD}{CE}$,列方程解答即可.
解答 解:(1)∵△ABC为正三角形,
∴∠B=∠C=60°,
∴∠ADB+∠BAD=120°,
∵∠ADB+∠CDE=120°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE.
(2)∵△ABD∽△DCE
∴$\frac{AB}{DC}=\frac{BD}{CE}$,
设正三角形边长为x,
则$\frac{x}{x-3}=\frac{3}{2}$,
解得x=9,
即△ABC的边长为9.
点评 本题考查了等边三角形性质,相似三角形的性质和判定,主要考查学生运用性质进行推理和计算的能力.能够证明△ABD∽△DCE是解决问题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
11.已知x=m是关于x的方程2x+m=6的解,则m的值是( )
| A. | -3 | B. | 3 | C. | -2 | D. | 2 |
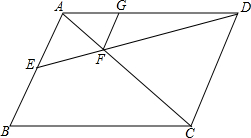 如图,?ABCD中,AB=6,E为AB中点,DE交AC于点F,FG∥AB交AD于点G,求线段FG的长.
如图,?ABCD中,AB=6,E为AB中点,DE交AC于点F,FG∥AB交AD于点G,求线段FG的长. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=30°.
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=30°.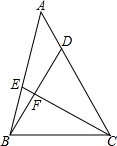 如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3.
如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3. 有一张一个角为30°,最小变长为4的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是8+4$\sqrt{3}$或16.
有一张一个角为30°,最小变长为4的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是8+4$\sqrt{3}$或16. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为( )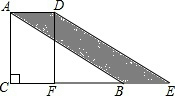 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于12,则平移距离等于( )
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于12,则平移距离等于( )