题目内容
 如图,AD=2,AC=4,BC=6,∠B=36°,∠D=107°,△ABC∽△DAC
如图,AD=2,AC=4,BC=6,∠B=36°,∠D=107°,△ABC∽△DAC(1)求AB的长;
(2)求CD的长;
(3)求∠BAD的大小.
考点:相似三角形的性质
专题:
分析:(1)由△ABC∽△DAC,根据相似三角形的对应边成比例,即可求得AB的长;
(2)由△ABC∽△DAC,根据相似三角形的对应边成比例,即可求得CD的长;
(3)由△ABC∽△DAC,根据相似三角形的对应角相等,即可求得∠BAD的大小.
(2)由△ABC∽△DAC,根据相似三角形的对应边成比例,即可求得CD的长;
(3)由△ABC∽△DAC,根据相似三角形的对应角相等,即可求得∠BAD的大小.
解答:解:(1)∵△ABC∽△DAC,
∴
=
,
∴
=
,
解得:AB=3;
(2)∵△ABC∽△DAC,
∴
=
,
∴
=
,
解得:CD=
;
(3)∵△ABC∽△DAC,
∴∠BAC=∠D=107°,∠CAD=∠B=36°,
∵∠B=36°,
∴∠BAD=∠BAC+∠CAD=107°+36°=143°.
∴
| AD |
| AB |
| AC |
| BC |
∴
| 2 |
| AB |
| 4 |
| 6 |
解得:AB=3;
(2)∵△ABC∽△DAC,
∴
| AC |
| BC |
| CD |
| AC |
∴
| 4 |
| 6 |
| CD |
| 4 |
解得:CD=
| 8 |
| 3 |
(3)∵△ABC∽△DAC,
∴∠BAC=∠D=107°,∠CAD=∠B=36°,
∵∠B=36°,
∴∠BAD=∠BAC+∠CAD=107°+36°=143°.
点评:此题考查了相似三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
将抛物线y=
x2的顶点向左平移
个单位长度,所得到的点的坐标是( )
| 1 |
| 3 |
| 1 |
| 3 |
A、(
| ||
B、(0,-
| ||
C、(0,
| ||
D、(-
|
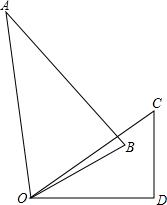 将一副含有60°角的三角板ABO的顶点O和另一块含有45°角的三角板CO′D的顶点O′重合,绕点O旋转三角板ABO,拼成如图情况,问:是否存在∠AOC,有∠AOC=3∠BOD?如果存在,求出∠AOD的度数,如果不存在,请说明理由.
将一副含有60°角的三角板ABO的顶点O和另一块含有45°角的三角板CO′D的顶点O′重合,绕点O旋转三角板ABO,拼成如图情况,问:是否存在∠AOC,有∠AOC=3∠BOD?如果存在,求出∠AOD的度数,如果不存在,请说明理由.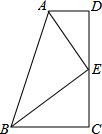 如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交DC于点E,连接BE,且AE⊥BE,求证:AB=AD+BC.
如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交DC于点E,连接BE,且AE⊥BE,求证:AB=AD+BC.